Study about Graph. What is Graph? Study & Analyze the motion of a Object Using Graphical Method with Interactive Simulation:

If information about various quantities related to motion is given in tabular form for various instant of time, it can be converted in g...

If information about various quantities related to motion is given in tabular form for various instant of time, it can be converted in graphical form. It makes easier for us to find out relation between various physical quantities. So Its necessary to study the motion of a body using graph. Now What is graph?
At first we see some graphs.in a Cricket score board. A match of 30 overs, first 10 overs the score was very slow, and gradually picked up in next 10 over then again slow the last 10 overs. In a TV we see a graph shown as below. 

Over	Score	Over	Score	Over	Score	Over	Score	Over	Score	Over	Score
1	2	6	9	11	20	16	44	21	68	26	90
2	3	7	10	12	24	17	55	22	69	27	101
3	5	8	12	13	29	18	60	23	70	28	111
4	6	9	14	14	35	19	65	24	72	29	121
5	7	10	15	15	40	20	67	25	82	30	128

A graph is a very powerful method of representing information. In a newspaper, magazine and on TV, we find graphs representing different information. In this table it shows the score at the end of each over in a thirty-over -one-day cricket match. The same information is presented in the form of a graph in this figure. Although the table and the graph contains exactly the same information, it is a lot easier to get an overall idea of how the scoring progressed from the graph. One can see at a glance from the graph that the scoring was very slow in the first 10 overs, it gradually picked up in the next 10 overs, it was again slow in the overs 20-25, and in the final 5 overs scoring was very fast.

Plotting a Graph: (How):

A graph is plotted to display the relation between two quantities. Generally, one of the two quantities change independently and the other quantities depends on it. For example we have consider two quantities, time and velocity. Here time is the independent quantity and velocity depends on it. To plot a graph from a table of values, the following steps are needed.

(A) Choosing the Axes: 

Draw two perpendicular lines, crossing each other at a point. Each line represents one of the two quantities to be plotted. Generally a horizontal line from left to right is drawn to represent the independent quantity, and a perpendicular line is drawn to represent the dependent quantity. These line are called the X-axis and Y-axis, of the horizontal axis and the vertical axis respectively. In this figure the OX represents the number of overs and the line OY represents the score. These lines are also named after the quantities they represents. Thus, in this figure the line OX is called the over axis and the line OY, the score axis.  

(B) Choosing the Scale:

The size on the paper on which a graph is drawn is limited on the available length of the axes, values are marked at equal distance. This is done in such way that all the value of the quantities represents on the axis can be accommodate in the available length.

(C) Plotting the Points:

Each set of values of the two quantities is represented by a point on the graph. To get this point, we mark the point corresponding to 8 overs on the over axis and draw a perpendicular on the over axis at this point. Similarly, we mark the point corresponding to 12 runs on the score axis and draw a perpendicular on the score axis at this point. The point of intersection of these perpendiculars is the point A, representing the set "8 overs, 12 runs".

(D) Joining the Points:

Once all the point corresponding to the available sets of values of the quantities are plotted. They are joined by a smooth curve to get the graph.

কোনও একটি বস্তুর অবস্থান জানতে হলে আরেকটি বস্তুর প্রয়োজন হয়। এই দ্বিতীয় বস্তুর সাপেক্ষে প্রথম বস্তুর অবস্থান নির্দিষ্ট করা যায়। তা না হলে বস্তুটির অবস্থান বলার কোনও অর্থ থাকে না। যখন একটি বস্তু স্থির বা সচল বলা হয়, তখন সবসময় ধরে নিতে হয় যে কোনও দ্বিতীয় বস্তুর সাপেক্ষে ওই বস্তুটি স্থির আছে অথবা ওর অবস্থান পরিবর্তিত হচ্ছে। এই দ্বিতীয় বস্তুটিকে বলা হয় নির্দেশ বস্তু (Reference Body)।
দ্বিতীয় কোনও বস্তু উল্লেখ না করে যদি বলা হয় যে "পাখিটি উড়ে গেল", এভাবে বললেও কোনও ভূল হয় না, কারণ এখানে পৃথিবীকে দ্বিতীয় বস্তু বলে ধরে নেওয়া হয়। অর্থাৎ পৃথিবীই হল নির্দেশ বস্তু (Reference Body)। 
একটি বস্তুর অবস্থান কোনো নির্দেশ বস্তু সাপেক্ষে জানতে হলে ওই নির্দেশ বস্তুর সঙ্গে একটি স্থানাঙ্ক সংস্থা (Co-ordinate System) যুক্ত আছে বলে কল্পনা করে নেওয়া হয়। একে নির্দেশ ফ্রেম (Reference Frame) বলে। 
এখন যেকোনও বস্তুকণার গতি এবং তার অবস্থান নির্দেশ করতে গেলে প্রাথমিকভাবে আমরা দুটি ভৌতরাশি যথা দূরত্ব (Distance) এবং সরণ (Displacement) ব্যবহার করি। 
এখানে কোনও একটি নির্দেশ তন্ত্রের সাপেক্ষে আমরা দূরত্ব ও সরণ হিসাব করি। এই দুটি ভৌতরাশি কোনও একটি নির্দেশ তন্ত্রে সময়ের সাপেক্ষে কিভাবে পরিবর্তিত হয় তা আমরা সরণ-সময় (Displacement-Time) বা দূরত্ব-সময় (Distance-Time) লেখচিত্রের সাহায্যে খুব সহজভাবে বর্ণনা করা যায়। এখানে X অক্ষ বরাবর সময়কে (Time) এবং Y অক্ষ বরাবর সরণ বা দূরত্বকে আঁকা হয়। এখানে সময় হল স্বাধীন রাশি (Independent Quantity) এবং সরণ বা দূরত্ব হল অধীন রাশি (Dependent Quantity)। এখানে সময় পরিবর্তনের সাথে সাথে বস্তুটির দূরত্ব বা সরণ পরিবর্তিত হয়।
এবার কোনও বস্তুকণা সময়ের সাপেক্ষে কোনও একটি নির্দিষ্ট দূরত্ব কত দ্রুত অতিক্রম করল (How fast or How Slow) তা বিচারের জন্য আমরা আবার দুটি ভৌতরাশি ব্যবহার করি, দ্রুতি (Seed) এবং বেগ (Velocity)। কোনও বস্তুকণা যেকোনো দিকে একক সময়ে যে দূরত্ব অতিক্রম করে তা হল দ্রুতি (Speed) এবং একটি নির্দিষ্ট দিকে যে দূরত্ব অতিক্রম করে তা হল গতিবেগ (Velocity)। এই সময়ের সাপেক্ষে দ্রুতি বা গতিবেগের পরিবর্তন  আমরা লেখচিত্রের সাহায্যে খুব সহজে বর্ণনা করতে পারি। এখানে সময় (Time) হল স্বাধীন রাশি (Independent Quantity)। এই সময়কে X অক্ষ অঙ্কন করে গতিবেগকে Y অক্ষ বরাবর অঙ্কন করা হয়। সময়ের সাথে সাথে কোনও বস্তুর গতিবেগ কিভাবে পরিবর্তিত হয় তা লেখচিত্রের সাহায্যে আমরা খুব সহজে বুঝতে পারি।

             We have seen that the position of a particle can be describe by two physical quantity distance and displacement. Also other information about various quantity related to motion is given in a tabular form for various instant of time, it can be converted in graphical form. It makes easier for us to understand and find out relation between various physical quantities. Now we can study various type of graph to describing their motion.

(1) Distance - Time Graph
(2) Displacement - Time Graph
(3) Speed - Time Graph
(4) Velocity - Time Graph
(5) Acceleration - Time Graph
Now we analyze some various type of Graph. 

                                                      Graph Type: A
----------------------------------------------------------------------------------------------

 Here the equation is:  \(y = 2x\)

Y	0	2	4	6	8	10
x	0	1	2	3	4	5

----------------------------------------------------------------------------------------------

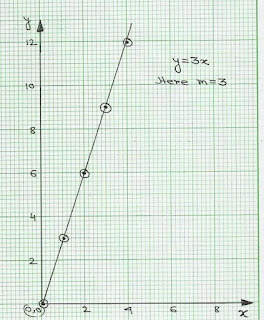
Here the equation is: \(y = 3x\)

Y	0	3	6	9	12	15
x	0	1	2	3	4	5

----------------------------------------------------------------------------------------------

Here The equation is:\(y = 4x\)

Y	0	4	8	12	16	20
x	0	1	2	3	4	5

----------------------------------------------------------------------------------------------

Now the above three graph are redraw in a graph paper simultaneously for more analysis.

\(y = 2x\)
\(y = 3x\)
\(y = 4x\)


Here we see that all graph passing through origin (0,0) and they are all straight line. Therefore we can generalize that \(y = mx\) is a straight line equation passing through origin.
Here m is a constant quantity called "slope" of the graph. Therefore \(m = \frac{y}{x}\).
If we change \(x\) to \(\Delta x\) and corresponding \(y\) change to \(\Delta y\), then we get \(m = \frac{{\Delta y}}{{\Delta x}}\)

From this figure we see that \(\tan \theta  = \frac{{AB}}{{OB}} = \frac{{OC}}{{OB}} = \frac{{\Delta y}}{{\Delta x}} = m\)
Thus slope (m)=\(\tan \theta \)

 
Conclusion: A general equation of a straight line passing through origin is \(y = mx\), where m is the slope of the graph and \(m = \tan \theta \), where \(\theta \) is the angle between graphs with X-axis. We see that \({\theta _1} < {\theta _2} < {\theta _3}\) where \({\theta _1},{\theta _2},{\theta _3}\) are the angle between the graph and horizontal axis.
----------------------------------------------------------------------------------------------
                                      Graph Type: 2
 Now we plot some another type of Graph:

Here the equation is: \(y = 2x + 2\)

Y	2	4	6	8	10	12
x	0	1	2	3	4	5

----------------------------------------------------------------------------------------------

Here the equation is: \(y = 3x + 2\)

Y	2	5	8	11	14	17
x	0	1	2	3	4	5

---------------------------------------------------------------------------------------------

Here the equation is: \(y = 4x + 2\)

Y	2	6	10	14	18	22
x	0	1	2	3	4	5

---------------------------------------------------------------------------------------------
Now the above three graph are redraw in a graph paper simultaneously for more analysis.

Here the equations are:
 \(y = 2x + 2\)
\(y = 3x + 2\)
\(y = 4x + 2\)

We see that all the graphs has different slope but a same constant quantity having same value. We can now these equation in a generalize form \(y = mx + c\), Where "m" is the slope of the graph and "c" is a constant quantity.
Here we can redraw the three graph in a same coordinate system. Here all the graph has different slope "m", but same constant quantities where the graph start from Y-axis. Hence the three graphs are starting from "Y=2" but have different slope means different angle with the X axis.
Conclusion: A general equation of a straight line and not passing through origin is \(y = mx + c\), where "m" is the slope of the curve and "c" is a constant quantity where the graph start fromY-axis.
----------------------------------------------------------------------------------------------

Here the equation is: \(y = 2x + 2\)

Y	2	4	6	8	10	12
x	0	1	2	3	4	5

-----------------------------------------------------------------------------------------------

Here equation is: \(y = 2x + 3\)

Y	3	5	7	9	11	13
x	0	1	2	3	4	5

------------------------------------------------------------------------------------------------

Here the equation is: \(y = 2x + 4\)

Y	4	6	8	10	12	14
x	0	1	2	3	4	5

-----------------------------------------------------------------------------------------
Now here we see that all graphs has same slope, means all graphs are straight line also and parallel to each other. We can also generalize the all equation by \(y = mx + c\), where 'm' is the slope of the graphs abnd "c" is a constant quantity. Hehe all the graph has same slope with value "2", but different constant quantity, where the graph start from Y-axis. Hence the three graph are parallel to each other due to same slope and have some constant value at "x = 0".

\(y = 2x + 2\)
\(y = 2x + 3\)
\(y = 2x + 4\)

Conclusion: A general equation of a straight line and not passing through origin is "\(y = mx + c\)", where 'm' is the slope of the graph and this slope (m) \(m = \tan \theta \), where \(\theta \) is the angle between graphs with the X-axis, and 'c' is a constant quantity when \(x = 0\)
-----------------------------------------------------------------------------------------
So, we learn here that
(1)  \(y = mx\) is a straight line equation passing through origin and the slope of the graph is "m" and \(m = \tan \theta \) where \(\theta \) is the angle between the straight line graph with X axis.

(2)  \(y = mx + c\) is also a straight line equation but its not passing the origin, it must pass the point at \(y = c\)  and slope of the graph \(m = \tan \theta \), where \(\theta \) is the angle between the graph with the axis.
-----------------------------------------------------------------------------------------
Now we consider a another type of graphs like that
\(\begin{array}{l}y = {x^2}\\y = 2{x^2}\\y = 3{x^2}\end{array}\) 
Here we draw a graph  \(y = 2{x^2}\)

Here the graph look likes a ellipse. Since its not a straight line equation, its slopes are different in different situation.







-----------------------------------------------------------------------------------------
Now we consider a graph  parallel to X-axis.

Here we calculate the slope of the graph.
Here slope (m) is
\(m = \frac{{\Delta y}}{{\Delta x}} = \frac{0}{{{x_2} - {x_1}}} = 0\)

So, a straight line parallel to X-axis has zero slope always.
-----------------------------------------------------------------------------------------
Now we consider a graph parallel to Y-axis.

Here we calculate the slope of the graph.
Here the slope (m) is
\(m = \frac{{\Delta y}}{{\Delta x}} = \frac{{{y_2} - {y_1}}}{0} = \infty \)

So, a straight line parallel to Y-axis has infinity slope always.







----------------------------------------------------------------------------------