Tips And Tricks to Solve The Mechanics Problems Using Free Body Diagram: Part: II

Free Body Diagram on Pulley An ideal pulley have three characteristics: (i) Mass-less  (ii) Smooth/Friction-less   (iii)Circular. A ...

Free Body Diagram on Pulley

An ideal pulley have three characteristics: (i) Mass-less 
(ii) Smooth/Friction-less  
(iii)Circular.

A pulley has three arm during its motion.

(1) Central arm is known as main arm.

(2) Handing two arm are known as side arm.

The pulleys can be studied under three possible cases. 

Case: I

Main arm is fixed while side arms are free to move. In this case net force acting on ideal pulley will always be zero. Because \(F = ma\), for ideal pulley \(m = 0\) and hence \(F = 0\)

Thus if the tension in the two side string is equal to \(T\), the tension in the main string will be equal to \(2T\).

Say, \({m_2} > {m_1}\)

Since the length of the string is fixed, so if \({m_2}\) comes down by a distance \(x\), \({m_1}\) will go up by \(x\) only. Therefore, acceleration of both the blocks are equal in magnitude and opposite direction.

Note: If \(a\) comes out positive then assumed direction of \(a\) is correct. If \(a\) comes out negative, then actual direction is opposite to the direction assumed.

Motion of a Connected Block Over a Mass-less and Friction-less Pulley Type: I

Two Body System:

Two Body System in Pulley Problems

FBD of First Mass

FBD of Second Mass

FBD of Pulley

Let two body \(A\) and \(B\) of mass \({m_1}\) and \({m_2}\) are connected at two ends of a mass-less in-extensible string passing over a friction-less pulley \(P\). Since mass of the pulley is zero then, tension of the string is equal for both side of the pulley. From free body diagram we get,
For mass \({m_1}\):
\({T_1} - {m_1}g = {m_1}a\)
For mass \({m_2}\):
\({m_2}g - {T_1} = {m_2}a\)
For pulley \(P\):
\({T_2} = 2{T_1}\)
From these equation we get,
\({m_2}g - \left( {{m_1}g + {m_1}a} \right) = {m_2}a\)
or, \(\left( {{m_1}a + {m_2}a} \right) = \left( {{m_2}g - {m_1}g} \right)\)
or, \(\left( {{m_2} + {m_1}} \right)a = \left( {{m_2} - {m_1}} \right)g\)
or, \(a = \frac{{\left( {{m_2} - {m_1}} \right)}}{{\left( {{m_2} + {m_1}} \right)}}g\)
And, tension of the string (same for both side of the pulley) \({T_1} = {m_1}a + {m_1}g = \frac{{{m_1}\left( {{m_2} - {m_1}} \right)}}{{\left( {{m_2} + {m_1}} \right)}}g + {m_1}g = \frac{{2{m_1}{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}g\)
And tension or thrust on the pulley is \({T_2} = 2{T_1} = \frac{{4{m_1}{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}g\)

Three Body System:
Let a body of mass \({m_1}\) and other two body B and C of masses \({m_2}\) and \({m_3}\) are connected of a mass-less string passing over a friction-less pulley \(P\). From free body diagram we can write,

FBD of Mass \({m_1}\)

FBD of Mass \({m_2}\)

FBD of Mass \({m_3}\)

For mass \({m_1}\):
\({T_1} - {m_1}g = {m_1}a\)
For mass \({m_2}\):
\({m_2}g + {T_2} - {T_1} = {m_2}a\)
For mass \({m_3}\):
\({m_3}g - {T_2} = {m_3}a\)
For pulley \(P\):
\({T_3} = 2{T_1}\)
From these equation we get, 
\(a = \frac{{\left[ {\left( {{m_2} + {m_3}} \right) - {m_1}} \right]}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}g\)
And tension of the string \({T_1} = \frac{{2{m_1}\left( {{m_2} + {m_3}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}g\)
And tension of the string \({T_2} = \frac{{2{m_1}{m_3}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}g\)
And tension or thrust on the pulley \({T_3} = 2{T_1} = \frac{{4{m_1}\left( {{m_2} + {m_3}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}g\)

When a body A of mass \({m_1}\) rests on a friction-less horizontal surface. Let a string passing over a pulley connect \({m_1}\) with a body B of mass \({m_2}\) as shown below:

From free body diagram we get,
For mass \({m_1}\):
\(T = {m_1}a\)
For mass \({m_2}\):
\({m_2}g - T = {m_2}a\)
From these two equation we get,
Acceleration \(a = \frac{{{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}g\)
Tension of the string \(T = \frac{{{m_1}{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}g\) And Tension or thrust on pulley \(P = \sqrt {{T^2} + {T^2}}  = \sqrt 2 T\)

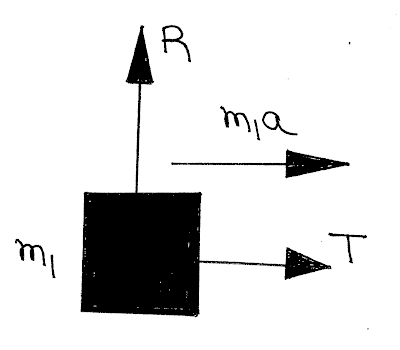
When a body A of mass \({m_1}\) rests on a horizontal surface with co-efficient of friction \(\mu \) between body and the table. Let a string passing over a pulley connect \({m_1}\) with a body B of mass \({m_2}\) as shown in below:

     
  

From free body diagram we get,
For mass \({m_1}\):
\(R = mg\) and \(T - \mu R = {m_1}a\)
or, \(T - \mu {m_1}g = {m_1}a\)
For mass \({m_2}\):
From these two equation,
Acceleration \(a = \frac{{\left( {{m_2} - \mu {m_1}} \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\) And tension of the string \(T = \frac{{{m_1}{m_2}\left( {1 + \mu } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\)  

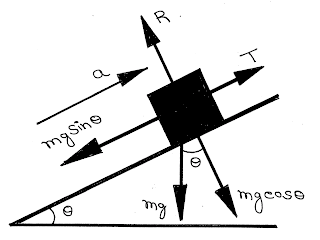
Two masses are suspended over a pulley on a friction-less inclined plane as shown below in the figure. The mass \({m_2}\) descends with an acceleration \(a\). The mass \({m_1}\) s on inclined plane:

From free body diagram we get,
For mass \({m_1}\):
\(T - {m_1}g\sin \theta  = {m_1}a\)
For mass \({m_2}\):
\({m_2}g - T = {m_2}a\)
From these equation we get,
Acceleration \(a = \frac{{\left( {{m_2} - {m_1}\sin \theta } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\) and,
Tension of the string \(T = \frac{{{m_1}{m_2}\left( {1 + \sin \theta } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\)

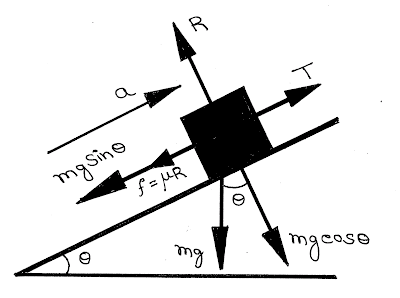
Two masses are suspended over a pulley on a inclined plane with coefficient of friction between the surface and the body is \(\mu \)as shown in figure below. The mass \({m_2}\) descends with an acceleration \(a\). The mass \({m_1}\) is on inclined plane:

From free body diagram we get,
For mass \({m_1}\):
\(R = {m_1}g\cos \theta \) and, \(T - \mu R - {m_1}g\sin \theta  = {m_1}a\)
For mass \({m_2}\):
\({m_2}g - T = {m_2}a\)
From these two equation we get,
Acceleration \(a = \frac{{\left[ {{m_1} - {m_1}\left( {\sin \theta  + \mu \cos \theta } \right)} \right]}}{{\left( {{m_1} + {m_2}} \right)}}g\) and,
Tension of the string \(T = \frac{{{m_1}{m_2}\left( {1 + \sin \theta  + \mu \cos \theta } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\)

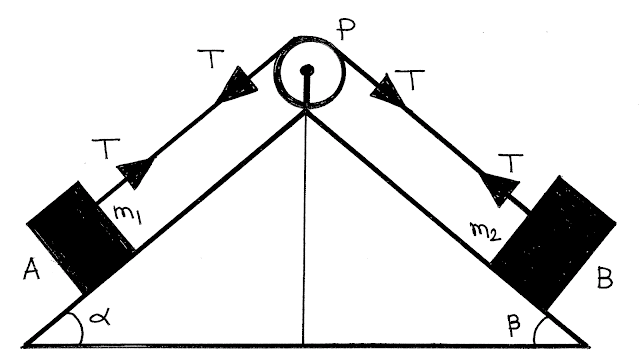
Two body A and B of masses \({m_1}\) and \({m_2}\) are connected by a string passing over a friction-less pulley such that \({m_2} > {m_1}\): 

From free body diagram we get, 
For mass \({m_1}\):
\(T - {m_1}g\sin \alpha  = {m_1}a\)
For mass \({m_2}\):
\({m_2}g\sin \beta  - T = {m_2}a\)
From these two equation we get,
Acceleration \(a = \frac{{\left( {{m_2}\sin \beta  - {m_1}\sin \alpha } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\) and,
Tension of the string \(T = \frac{{{m_1}{m_2}\left( {\sin \alpha  + \sin \beta } \right)}}{{\left( {{m_1} + {m_2}} \right)}}g\)

The mass \(M\) is connected to \({m_1}\) and \({m_2}\) via string passing over alight pulleys. Let \({m_1} > {m_2}\). Obviously \({m_1}\) moves down an acceleration \(a\). The block on the horizontal table moves towards right with acceleration \(a\):

From free body Diagram we get,
For mass \({m_1}\):
\({m_1}g - {T_1} = {m_1}a\)
For mass \({m_2}\):
\({T_2} - {m_2}g = {m_2}a\)
For mass \(M\):
\({T_1} - {T_2} = Ma\)
From these equation we get,
Acceleration \(a = \frac{{\left( {{m_1} - {m_2}} \right)}}{{\left( {{m_1} + {m_2} + M} \right)}}g\) and,
Tension of the string \({T_1} = \frac{{{m_1}\left( {2{m_2} + M} \right)}}{{\left( {{m_1} + {m_2} + M} \right)}}g\) and,
Tension of the string \({T_2} = \frac{{{m_2}\left( {2{m_1} + M} \right)}}{{\left( {{m_1} + {m_2} + M} \right)}}g\)