Electric Current, Potential Difference & EMF: Concept of Electric Charge, Electric Potential Difference, EMF and Electric Cell...
Electric Current, Potential Difference & EMF:
Concept of Electric Charge, Electric Potential Difference, EMF and Electric Cell as a source of EMF, Concept of Electric Current, Relation between Potential difference and current in a wire, Concept of resistance from Ohm's Law, EMF and internal resistance of a cell, Resistivity and Conductivity, Series and Parallel Combination of Resistance, Domestic circuits.
তড়িৎআধানের ধারণা (Concept of Charge):
ভর কাকে বলে তা আমরা জানি। কোনও বস্তুর মধ্যে যতখানি জড় পদার্থ থাকে, তাকে ওই বস্তুর ভর বলে। কিন্তু ভরকে কি চোখে দেখা যায়? উত্তর না। এই ভর শুধুমাত্র একটি ধারণা (Concept)। এই ভরের ধারণা সর্বপ্রথম দেন বিজ্ঞানী আইজ্যাক নিউটন তার মহাকর্ষীয় সূত্রে। তার সূত্র থেকেই পাই কোনও পদার্থের একটি মৌলিক কণা অপর একটি মৌলিক কণাকে আকর্ষণ করে শুধুমাত্র তাদের ভরের জন্য। তাই ভর একটি ধারণামাত্র।
তেমনি একটি তড়িৎগ্রস্থ বস্তু অপর একটি তড়িৎগ্রস্থ বস্তুর মধ্যে আকর্ষণ বা বিকর্ষণ বল ক্রিয়া করে পদার্থের অপর একটি ধারণার জন্য, তা হল তড়িতাধান (Electric Charge)। এই তড়িৎআধানও চোখে দেখার মতো বস্তু নয়। এটিও একটি ধারণামাত্র, কিন্তু পরিমাপযোগ্য ভৌতরাশি। তাই বলাযায়, পদার্থের যে মৌলিক ধর্মের জন্য তড়িৎবল (আকর্ষণ বা বিকর্ষণ) ক্রিয়া করে তাকে তড়িতাধান বলে। এই তড়িতাধান কোনও বস্তুর সঙ্গে সম্পর্কযুক্ত হলে, ওই বস্তুর চারিপাশে তড়িৎক্ষেত্র ও চৌম্বকক্ষেত্র সৃষ্টি হয়। তাই তড়িতাধানের সংজ্ঞা হিসাবে বলা যায় যে,
তড়িতাধান (Electric Charge):
তড়িৎশক্তির বাস্তব রূপ বা প্রকাশকে তড়িতাধান বলে। এই তড়িতাধান হল কোনও বস্তু বা বস্তুসমষ্টির এমন একটি ভৌতধর্ম যার জন্য ওই বস্তু অপর কোনও বস্তুর সাথে সম্পর্কযুক্ত হলে, তাদের মধ্যে তড়িৎবল ক্রিয়া করে এবং ওই বস্তুর চারিপাশে একটি তড়িৎক্ষেত্র ও চৌম্বকক্ষেত্র সৃষ্টি হয়।
তড়িতাধানের উৎস (Origin of Electric Charge):
আমরা জানি যেকোনও বস্তু বা কোনও বস্তুর পরমাণু তড়িৎ নিরপেক্ষ হয়। কারণ ওই পরমাণুর নিউক্লিয়াসের অভ্যন্তরে যতগুলি ধনাত্বক তড়িৎ সম্পন্ন প্রোটন কণিকা থাকে, নিউক্লিয়াসের াইরে ঠিক ততগুলিই ঋনাত্বক তড়িৎসম্পন্ন ইলেকট্রন কণিকা থাকে। এবং একটি প্রোটন ও একটি ইলেকট্রনের তড়িতাধানের মান সমান কিন্তু বিপরীত। তাই সাধারণ অবস্থায় যেকোনও বস্তু তড়িৎ নিরপেক্ষ হয়।
এখন কোনও কারণে ওই পরমাণুর বাইরের কক্ষপথ থেকে এক বা একাধিক ইলেকট্রন কোথাও চলে গেলে বা ওই পরমাণুর ঋনাত্বক তড়িতের ইলেকট্রন অপেক্ষা ধনাত্বক তড়িতের প্রোটন সংখ্যা বেড়ে যায়। তখন বস্তুটি তড়িতাহিত হয়ে ড়ে। আবার একইরকম কোনও কারণে কোনও বস্তুর পরমাণুর বাইরের কক্ষপথে বাইরে থেকে এক বা একাধিক ইলেকট্রন এসে যুক্ত হলে, ওই বস্তুর ধনাত্বক তড়িতের প্রোটন কণিকা অপেক্ষা ঋনাত্বক তড়িতের ইলেকট্রন সংখ্যা বেড়ে যায়। তখনও বস্তুটি তড়িতাহিত হয়ে পড়ে। তাহলে এটা বোঝা যায় যে, কোনও বস্তু তড়িতাহিত হওয়া নির্ভর করে, ওই পরমাণুর বাইরের কক্ষপথের ইলেকট্রনের আদান প্রদানের উপর।
এখন ধরাযাক, কোনও পরমাণুর ইলেকট্রন সংখ্যা \({n_e}\) এবং প্রোটন সংখ্যা \({n_p}\)।
যদি কোনও পরমাণুতে বাইরে থেকে ইলেকট্রন এসে যুক্ত হয়, তখন \({n_e} > {n_p}\)। তখন বস্তুটি ঋনাত্বক তড়িৎগ্রস্থ হয়। আবার যদি কোনও পরমাণু থেকে ইলেকট্রন চলে যায় তখন \({n_e} < {n_p}\)। তখন বস্তুটি ধনাত্বক তড়িৎগ্রস্থ হয়।
এখন আমরা জানি একটি ইলেকট্রনের ভর (\({m_e} = 9.1 \times {10^{ - 31}}kg\))। এখন কোনও বস্তু ঋনাত্বক তড়িতে আহিত হলে তার ভর সামান্য বাড়ে কারণ \(n\) সংখ্যক ইলেকট্রন বাইরে থেকে এসে যুক্ত হয়, তার ফলে \(\left( {n \times {m_e}} \right)\) পরিমাণ বৃদ্ধি পায়।
আবার যখন, বস্তুটি ধনাত্বক তড়িতে আহিত হয় তখন \(n\) সংখ্যক ইলেকট্রন চলে যাওয়ার জন্য তার ভর সামান্য পরিমান \(\left( {n \times {m_e}} \right)\) কমে যায়। তাই তড়িতাধান সর্বদা ভরের সাথে সম্পর্কযুক্ত হবেই।
 |
| নিস্তড়িৎ বস্তু |
 |
| ধনাত্বক তড়িৎগ্রস্থ বস্তু |
 |
| ঋনাত্বক তড়িৎগ্রস্থ বস্তু |
তড়িতাধানের প্রকারভেদ (Types of Charge):
তড়িতাধান দুই ধরণের হতে পারে।
তড়িতাধানের ধর্ম (Properties of Electric Charge):
- [vtab]
- ধনাত্বক তড়িৎ (Positive Charge)
- (i) কোনও নিস্তড়িৎ পরমাণুর বাইরের কক্ষপথ থেকে ইলেকট্রন চলে গেলে ধনাত্বক তড়িতের উদ্ভব ঘটে অর্থাৎ কোনও পরমাণুর প্রোটন সংখ্যা অপেক্ষা ইলেকট্রন সংখ্যা কম থাকলে ধনাত্বক তড়িৎ এর সৃষ্টি হয়। (ii) নিস্তড়িৎ পরমাণু থেকে ইলেকট্রন চলে যাওয়ায় ধনাত্বক তড়িৎগ্রস্থ পরমাণুটির ভর সামান্য পরিমান হ্রাস পায়। (iii) একটি কাঁচের দন্ডকে সিল্ক দ্বারা ঘর্ষন করলে কাঁচ দন্ডটি থেকে সিল্কে ইলেকট্রন চলে যায়, তাই কাঁচদন্ডটি ধনাত্বক তড়িতে আহিত হয়।
- ঋনাত্বক তড়িৎ (Negative Charge)
- (i) কোনও নিস্তড়িৎ পরমাণুর বাইরের কক্ষপথে ইলেকট্রন এসে প্রবেশ করলে ঋনাত্বক তড়িতের উদ্ভব ঘটে অর্থাৎ কোনও পরমাণুর ইলেকট্রন সংখ্যা অপেক্ষা প্রোটন সংখ্যা কম থাকলে ঋনাত্বক তড়িতের সৃষ্টি হয়। (ii) নিস্তড়িৎ পরমাণুতে ইলেকট্রন এসে প্রবেশ করার জন্য নাত্বক তড়িৎগ্রস্থ পরমাণুটির ভর সামান্য বৃদ্ধি পায় (iii) একটি এবোনাইট দন্ডকে ফার দ্বারা ঘর্ষণ করলে ইলেকট্রন এবোনাইটে চলে আসে তাই এবোনাইট দন্ডটি ঋনাত্বক তড়িতে আহিত হয়।
তড়িতাধানের ধর্ম (Properties of Electric Charge):
(1) কোনও তড়িতাহিত বস্তুকে একটি অনাহিত বস্তুর সংস্পর্শে আনলে, তড়িতাহিত বস্তু থেকে অনাহিত বস্তুতে আধান স্থানান্তরিত হয়।
(2) আধা সর্বদা ভরের সাথে সম্পর্কযুক্ত হবেই। কোনও নিস্তড়িৎ পরমাণু আধানগ্রস্থ হলে তার ভর হয় কমে না হয় বাড়ে।
(3) কোনও বস্তুর আধান সর্বদা সংরক্ষিত থাকবেই।
অর্থাৎ তড়িৎ আধানকে সৃষ্টি বা ধ্বংস করা যায় না। শুধুমাত্র একটি বস্তু থেকে অন্য বস্তুতে আধানের স্থানান্তরন ঘটে মাত্র। যেমন,
একটি তেজস্ক্রিয় ভাঙনে একটি ইউরেনিয়ামের নিউক্লিয়াস থোরিয়াম নিউক্লিয়াসে পরিনত হয় এবং একটি আলফা কণা নির্গত হয়। কিন্তু মোট আধান সর্বদা সংরক্ষিত থাকে।
\(U_{92}^{238} \to Th_{90}^{234} + He_2^4\)
(4) তড়িতাধান, ভরের ন্যায় বস্তুর গতিবেগের সাথে সম্পর্কযুক্ত নয়।
(5) কোনও তড়িতাধান স্থির থাকলে তার চারিপাশে একটি তড়িৎক্ষেত্র সৃষ্টি হয়, তড়িতাধানটি সমবেগে গতিশীল থাকলে তড়িৎক্ষেত্র ও চৌম্বকক্ষেত্র উভয়ই সৃষ্টি হয় আবার তড়িতাধানটি ত্বরণ বা মন্দনসহ গতিশীল থাকলে তড়িৎক্ষেত্র, চৌম্বকক্ষেত্র এবং তড়িৎচুম্বকীয় বিকিরণ নির্গত করে।
(6) তড়িতাধান সর্বদা পরিবাহীর পৃষ্ঠতলে অবস্থান করে। সমপ্রকৃতির আধান পরস্পর পরস্পরকে বিকর্ষণ করার জন্য আধান পরিবাহীর পৃষ্ঠে চলে যায়।
(7) কোনও বস্তুর তড়িতাধান যেকোনও মানের হতে পারে না। এই তড়িতাধানের মান সর্বদা একটি ইলেকট্রনের আধানের মানের সরল গুনিতক হয়। অর্থাৎ কোনও বস্তুর আধান \(Q\) হলে, \(Q = ne\), যেখানে \(n\) একটি পূর্নসংখ্যা এবং \(e\) একটি ইলেকট্রনের আধানের মানের সমান হয়।
(8) সম আধান পরস্পর পরস্পরকে বিকর্ষণ করে এবং বিপরীত আধান পরস্পর পরস্পকে আকর্ষণ করে।
(9) তড়িতাধান একটি স্কেলার রাশি।
তড়িতাধানের একক (Unit of Electric Charge):
স্থির তড়িতে একটি ইলেকট্রনের আধানের মানকেই সর্বনিম্ন ধরা হয় এবং একটি ইলেকট্রনের আধানের মান \(1.6 \times {10^{ - 19}}C\)। তাই SI পদ্ধতিতে তড়িতাধানের একক হল কুলম্ব (C)।
এবং
\(1.6 \times {10^{ - 19}}C\) হল একটি ইলেকট্রনের আধানের মান
সুতরাং \(1C\) হল \(\frac{1}{{1.6 \times {{10}^{ - 19}}}}\) টি ইলেকট্রনের আধানের মানের সমান।
অর্থাৎ \(1C\) হল \(6.25 \times {10^{18}}\) টি ইলেকট্রনের আধানের মানের সমান।
তাই কুলম্বের সংজ্ঞা হিসাবে বলা যায় যে, \(6.25 \times {10^{18}}\) টি ইলেকট্রনের আধানকে \(1\) কুলম্ব বলে।
কিছু ব্যবহারিক একক:
\(1mC = {10^{ - 3}}C\)
\(1\mu C = {10^{ - 6}}C\)
\(1nC = {10^{ - 9}}C\)
CGS পদ্ধতিতে তড়িতাধানের একক হল: স্ট্যাটকুলম্ব বা esu of Charge.
SI পদ্ধতিতে তড়িতাধানের একক কুলম্ব এবং CGS পদ্ধতিতে তড়িতাধানের এককের মধ্যে সম্পর্ক:
\(1C = 3 \times {10^9}esu = \frac{1}{{10}}emu\)
তড়িতাধানের আকর্ষণ ও বিকর্ষণ বল সংক্রান্ত কুলম্বের সূত্র (Coulomb's Law):
দুটি বিন্দু আধানের জন্য পারস্পরিক আকর্ষণ বা বিকর্ষণ বল, আধানদুটির মানের গুনফলের সমানুপাতিক এবং তাদের মধ্যকার দূরত্বের বর্গের ব্যাস্তানুপাতিক।
ধরাযাক, দুটি বিন্দু আধান \({Q_1}\) এবং \({Q_2}\) বায়ুমাধ্যমে \(r\) দূরত্বে রাখা আছে। কুলম্বের সূত্রানুযায়ী, আকর্ষণ বা বিকর্ষণ বল \(F\) হলে,
\(F \propto {Q_1}{Q_2}\) ... ... ... (i) এবং
\(F \propto \frac{1}{{{r^2}}}\) ... ... ... (ii)
এখন যৌগিক ভেদের নিয়মানুযায়ী (i) ও (ii) সমীকরণ থেকে পাই,
\(F \propto \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
বা, \(F = {k_1}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\) [এখানে \({k_1}\) হল একটি সমানুপাতিক ধ্রুবক, যার মান পারিপার্শ্বিক মাধ্যম ও একক পদ্ধতির উপর নির্ভর করে]
(a) এখন আধান দুটি শূন্য বা বায়ুমাধ্যমে থাকলে, CGS পদ্ধতিতে \({k_1} = 1\) হয়, তখন কুলম্বের সূত্রটি হয়, \(F = \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
(b) আধান দুটি বায়ু বা শূন্য মাধ্যমে থাকলে, SI পদ্ধতিতে এর মান হয় \({k_1} = \frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}\), যেখানে \({\varepsilon _0}\) হয় বায়ু বা শূন্য মাধ্যমের তড়িৎভেদ্যতা। তখন কুলম্বের সূত্রটি হয় \(F = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{Q_1}{Q_2}}}{{{r^2}}} = 9 \times {10^9} \times \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
(c) আধানদুটি অন্য কোনো মাধ্যমে অবস্থিত হলে, কুলম্বের সূত্রটি হয়, \(F = \frac{1}{{4\pi \varepsilon }}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\), যেখানে \(\varepsilon \) হল ওই মাধ্যমের তড়িৎভেদ্যতা।
[কোনও মাধ্যমের তড়িৎভেদ্যতা কি জিনিস সেটা উচ্চতর শ্রেণিতে আমরা শিখবো]
একক আধানের সংজ্ঞা:
তড়িৎ বিভবের ধারণা (Concept of Electric Potential):
 |
| Two Charge Separated by a distance |
\(F \propto {Q_1}{Q_2}\) ... ... ... (i) এবং
\(F \propto \frac{1}{{{r^2}}}\) ... ... ... (ii)
এখন যৌগিক ভেদের নিয়মানুযায়ী (i) ও (ii) সমীকরণ থেকে পাই,
\(F \propto \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
বা, \(F = {k_1}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\) [এখানে \({k_1}\) হল একটি সমানুপাতিক ধ্রুবক, যার মান পারিপার্শ্বিক মাধ্যম ও একক পদ্ধতির উপর নির্ভর করে]
(a) এখন আধান দুটি শূন্য বা বায়ুমাধ্যমে থাকলে, CGS পদ্ধতিতে \({k_1} = 1\) হয়, তখন কুলম্বের সূত্রটি হয়, \(F = \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
(b) আধান দুটি বায়ু বা শূন্য মাধ্যমে থাকলে, SI পদ্ধতিতে এর মান হয় \({k_1} = \frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}\), যেখানে \({\varepsilon _0}\) হয় বায়ু বা শূন্য মাধ্যমের তড়িৎভেদ্যতা। তখন কুলম্বের সূত্রটি হয় \(F = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{Q_1}{Q_2}}}{{{r^2}}} = 9 \times {10^9} \times \frac{{{Q_1}{Q_2}}}{{{r^2}}}\)
(c) আধানদুটি অন্য কোনো মাধ্যমে অবস্থিত হলে, কুলম্বের সূত্রটি হয়, \(F = \frac{1}{{4\pi \varepsilon }}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\), যেখানে \(\varepsilon \) হল ওই মাধ্যমের তড়িৎভেদ্যতা।
[কোনও মাধ্যমের তড়িৎভেদ্যতা কি জিনিস সেটা উচ্চতর শ্রেণিতে আমরা শিখবো]
একক আধানের সংজ্ঞা:
- [vtab]
- CGS পদ্ধতিতে একক আধানের সংজ্ঞা:
- আমরা জানি \(F = \frac{{{Q_1}{Q_2}}}{{{r^2}}}\), এখন \({Q_1} = {Q_2} = Q\) এবং \(r = 1\) ও \(F = 1\) হলে লেখা যায়, \({Q^2} = 1\) বা, \(Q = \pm 1\) হয়। তাই বলা যায়, বায়ু বা শূন্য মাধ্যমে একই প্রকৃতির ও সমমানের দুটি বিন্দু আধান পরস্পর থেকে \(1\) সেমি দূরত্বে থাকলে যদি তারা \(1\) ডাইন বিকর্ষণ বল অনুভব করে, তখন প্রত্যেকটি আধানকে CGS পদ্ধতিতে একক আধান বলা হয়।
- SI পদ্ধতিতে একক আধানের সংজ্ঞা
- আমরা জানি \(F = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{Q_1}{Q_2}}}{{{r^2}}} = 9 \times {10^9} \times \frac{{{Q_1}{Q_2}}}{{{r^2}}}\), এখন \({Q_1} = {Q_2} = Q\) এবং \(r = 1\) ও \(F = 9 \times {10^9}N\) হলে \({Q^2} = 1\) এবং \(Q = \pm 1\), তাই বলা যায় বায়ু বা শূন্য মাধ্যমে একই প্রকৃতির ও সমমানের দুটি বিন্দু আধান পরস্পর থেকে \(1m\) দূরে থাকলে তাদের মধ্যে যদি \(9 \times {10^9}N\) বিকর্ষণ বল অনুভব করে, তখন প্রত্যেকটি আধানকে SI পদ্ধতিতে একক আধান বলা হয়।
তড়িৎ বিভবের ধারণা (Concept of Electric Potential):
আমরা জানি সম প্রকৃতির আধান পরস্পরকে বিকর্ষণ করে এবং বিপরীত প্রকৃতির আধান পরস্পরকে আকর্ষণ করে। তাই কোনও একটি আধান কে অপর কোনও আধানের কাছে আনতে গেলে বা দূরে সরাতে গেলে আমাদেরকে বাইরে থেকে কিছুটা কাজ করতে হয়। এখন কোনও একটি স্থানে একটি তড়িতাধান রাখা থাকলে তার চারিপাশের অঞ্চলে একটি ক্ষেত্র তৈরি হয় যেখানে অপর কোনও আধান আনলে আমরা আকর্ষণ বা বিকর্ষণ বল অনুভব করি। স্থির তড়িতের ক্ষেত্রে এই অঞ্চলকে বলা হয় তড়িৎক্ষেত্র। এই তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে অপর কোনও আধান নিয়ে এলে প্রথম আধানটির জন্য সৃষ্ট তড়িৎক্ষেত্রের আকর্ষণ বা বিকর্ষণ বলের বিরূদ্ধে আমাদেরকে কার্য করতে হয়। সাধারণত অসীমে একটি ধনাত্বক তড়িতের স্থিতিশক্তিকে শূন্য বলে ধরে নেওয়া হয়। তাই কোনও একক ধনাত্বক আধানকে অসীম থেকে কোনও তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে নিয়ে আসতে যে পরিমান কার্য করতে হবে তার দ্বারা তড়িৎবিভব পরিমাপ করা হয়। এই তড়িৎবিভব একটি স্কেলার রাশি।
 |
| কোনও বিন্দুতে তড়িৎ বিভব |
তড়িৎ বিভবের সংজ্ঞা (Electric Potential):
অসীম দূরত্ব থেকে একটি একক মানের ধনাত্বক আধানকে তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে নিয়ে আসতে যে পরিমান কার্য সম্পাদন করতে হয়, তাকে ওই বিন্দুর তড়িৎ বিভব বলে।
ধনাত্বক আধানযুক্ত পরিবাহীর বিভবকে ধনাত্বক বিভব বা উচ্চ বিভব এবং ঋনাত্বক আধানযুক্ত পরিবাহীর বিভবকে ঋনাত্বক বিভব বা নিম্ন বিভব বলে ধরা হয়।
ধরাযাক, কোনও তড়িৎক্ষেত্রে অবস্থিত \(P\) একটি বিন্দু। এখন একটি \(Q\) মানের ধনাত্বক আধানকে অসীম দূরত্ব থেকে এই \(P\) বিন্দুতে নিয়ে আনতে যদি \(W\) পরিমান কার্য করতে হয় তাহলে, সংজ্ঞানুযায়ী \(P\) বিন্দুতে তড়িত বিভব \({V_P}\) হলে লেখা যায়,
\({V_p} = \frac{{Work - done}}{{Ch\arg e}} = \frac{W}{Q}\)
অর্থাৎ তড়িৎ বিভব = সম্পাদিত কৃতকার্য/আধান
তড়িৎ বিভবের একক ও মাত্রা (Unit and Dimension of Electric Potential):
আমরা জানি, \(V = \frac{W}{Q}\)
CGS ও SI পদ্ধতিতে তড়িৎ বিভবের মধ্যে সম্পর্ক:
ধরাযাক কোনও স্থির তড়িৎক্ষেত্রে \(P\) এবং \(Q\) দুটি বিন্দু। এই \(P\) ও \(Q\) বিন্দুর বিভব যথাক্রমে \({V_P}\) এবং \({V_Q}\)। অর্থাৎ একটি ধনাত্বক আধান \(Q\) কে অসীম দূরত্ব থেকে \(P\) বিন্দুতে নিয়ে আসতে সম্পাদিত কৃতকার্য \({V_P} = \frac{{{W_P}}}{Q}\) এবং অসীম থেকে \(Q\) বিন্দুতে নিয়ে আসতে সম্পাদিত কৃতকার্য \( = {V_Q} = \frac{{{W_Q}}}{Q}\)
এখন ওই আধানটিকে \(P\) বিন্দু থেকে \(Q\) বিন্দুতে নিয়ে আসতে কৃতকার্য \( = \left( {{V_Q} - {V_P}} \right) = {V_{PQ}} = \Delta V = \left( {\frac{{{W_Q}}}{Q} - \frac{{{W_P}}}{Q}} \right) = \left( {\frac{{{W_Q} - {W_P}}}{Q}} \right) = \frac{{{W_{PQ}}}}{Q} = \frac{{\Delta W}}{Q}\)
বা, \(\left( {{V_Q} - {V_P}} \right) = \frac{{{W_{PQ}}}}{Q}\)
বা, \({W_{PQ}} = Q\Delta V\)
বা, \(\Delta V = \frac{{\Delta W}}{Q}\)
এই সমীকরণ থেকে বোঝা যায় যে,
(i) \({W_{PQ}}\) ধনাত্বক হলে \({V_Q} > {V_P}\)
(ii) \({W_{PQ}}\) ঋনাত্বক হলে \({V_Q} < {V_P}\)
(iii) \({W_{PQ}} = 0\) হলে \({V_Q} = {V_P}\)
বিভব পার্থ্যকের সংজ্ঞা (Definition of Electric Potential):
একটি একক মানের ধনাত্বক আধানকে তড়িৎক্ষেত্রের বা কোনও পরিবাহীর একটি বিন্দু থেকে অপর কোনও একটি বিন্দুতে নিয়ে আসতে যে পরিমাণ কার্য করতে হয়, তাকে ওই দুই বিন্দুর বিভব পার্থক্য বা বিভব প্রভেদ বলে।
বিভব প্রভেদের একক ও মাত্রা:
CGS পদ্ধতিতে বিভব প্রভেদের একক হল: esu of potential বা স্ট্যাটভোল্ট
SI পদ্ধতিতে বিভব প্রভেদের একক হল: ভোল্ট (volt)
তড়িৎচ্চালক বলের ধারণা (Concept of Electromotive Force):
অসীম দূরত্ব থেকে একটি একক মানের ধনাত্বক আধানকে তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে নিয়ে আসতে যে পরিমান কার্য সম্পাদন করতে হয়, তাকে ওই বিন্দুর তড়িৎ বিভব বলে।
ধনাত্বক আধানযুক্ত পরিবাহীর বিভবকে ধনাত্বক বিভব বা উচ্চ বিভব এবং ঋনাত্বক আধানযুক্ত পরিবাহীর বিভবকে ঋনাত্বক বিভব বা নিম্ন বিভব বলে ধরা হয়।
ধরাযাক, কোনও তড়িৎক্ষেত্রে অবস্থিত \(P\) একটি বিন্দু। এখন একটি \(Q\) মানের ধনাত্বক আধানকে অসীম দূরত্ব থেকে এই \(P\) বিন্দুতে নিয়ে আনতে যদি \(W\) পরিমান কার্য করতে হয় তাহলে, সংজ্ঞানুযায়ী \(P\) বিন্দুতে তড়িত বিভব \({V_P}\) হলে লেখা যায়,
\({V_p} = \frac{{Work - done}}{{Ch\arg e}} = \frac{W}{Q}\)
অর্থাৎ তড়িৎ বিভব = সম্পাদিত কৃতকার্য/আধান
তড়িৎ বিভবের একক ও মাত্রা (Unit and Dimension of Electric Potential):
আমরা জানি, \(V = \frac{W}{Q}\)
- [vtab]
- CGS পদ্ধতিতে তড়িৎবিভবের একক:
- CGS পদ্ধতিতে কৃতকার্যের একক হল আর্গ (erg) এবং তড়িতাধানের একক esu of charge, তাই CGS পদ্ধতিতে তড়িৎবিভবের একক হল erg/esu of charge = esu of potential বা স্ট্যাটভোল্ট (stat-volt), তাই বলা যায় 1 esu মানের একটি ধনাত্বক তড়িতাধানকে অসীম থেকে তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে নিয়ে আসতে যদি 1 erg কার্য সম্পাদন করতে হয়, তাহলে ওই বিন্দুর বিভব 1 esu of potential বলে
- SI পদ্ধতিতে তড়িৎবিভবের একক:
- SI পদ্ধতিতে কৃতকার্যের একক হল জুল (joule) এবং তড়িতাধানের একক কুলম্ব (C), তাই SI পদ্ধতিতে তড়িৎবিভবের একক হল = জুল/কুলম্ব = ভোল্ট। বা \(1V = \frac{{1joule}}{{1coulomb}}\), তাই লেখা যায়, এক কুলম্ব ধনাত্বক তড়িতাধানকে অসীম দূরত্ব থেকে তড়িৎক্ষেত্রের কোনও একটি বিন্দুতে নিয়ে আসতে যদি এক জুল কার্য সম্পাদন করতে হয়, তাহলে ওই বিন্দুর বিভবকে 1 ভোল্ট বিভব বলে।
CGS ও SI পদ্ধতিতে তড়িৎ বিভবের মধ্যে সম্পর্ক:
\(1V = \frac{{1J}}{{1C}} = \frac{{{{10}^7}erg}}{{3 \times {{10}^9}esu}} = \frac{1}{{300}}esu - of - potential\)
বা, \(1V = \frac{1}{{300}}esu\)
বা, \(1esu = 300V\)
পৃথিবীর তড়িৎ বিভব:
পৃথিবীর তড়িৎবিভবকে সর্বদা শূন্য বলে ধরা হয়। কারণ পৃথিবী নিজেই একটি নির্দিষ্ট বিভব যুক্ত ইলেকট্রনের বিরাট আধার। এবং তড়িতের সুপরিবাহী। এখানে কিছু ইলেকট্রন যোগ করলে বা পৃথিবী থেকে কিছু ইলেকট্রন বেরিয়ে গেলে ওর বিভব বাড়েও না বা কমেও না। পৃথিবীর তড়িৎবিভব সবসময় অপরিবর্তিত থাকে বলে পৃথিবীর বিভবকে শূন্য হিসাবে ধরা হয়। এই পৃথিবীর সাপেক্ষে কোনও বস্তুর বিভব উচ্চ বা নিম্ন হলে বস্তুটির বিভব যথাক্রমে ধনাত্বক বা ঋনাত্বক বিভব যুক্ত বলা হয়।
বিভব পার্থক্যের ধারণা (Concept of Potential Difference):
 |
| P ও Q বিন্দুর মধ্যে বিভব পার্থক্য |
এখন ওই আধানটিকে \(P\) বিন্দু থেকে \(Q\) বিন্দুতে নিয়ে আসতে কৃতকার্য \( = \left( {{V_Q} - {V_P}} \right) = {V_{PQ}} = \Delta V = \left( {\frac{{{W_Q}}}{Q} - \frac{{{W_P}}}{Q}} \right) = \left( {\frac{{{W_Q} - {W_P}}}{Q}} \right) = \frac{{{W_{PQ}}}}{Q} = \frac{{\Delta W}}{Q}\)
বা, \(\left( {{V_Q} - {V_P}} \right) = \frac{{{W_{PQ}}}}{Q}\)
বা, \({W_{PQ}} = Q\Delta V\)
বা, \(\Delta V = \frac{{\Delta W}}{Q}\)
এই সমীকরণ থেকে বোঝা যায় যে,
(i) \({W_{PQ}}\) ধনাত্বক হলে \({V_Q} > {V_P}\)
(ii) \({W_{PQ}}\) ঋনাত্বক হলে \({V_Q} < {V_P}\)
(iii) \({W_{PQ}} = 0\) হলে \({V_Q} = {V_P}\)
বিভব পার্থ্যকের সংজ্ঞা (Definition of Electric Potential):
একটি একক মানের ধনাত্বক আধানকে তড়িৎক্ষেত্রের বা কোনও পরিবাহীর একটি বিন্দু থেকে অপর কোনও একটি বিন্দুতে নিয়ে আসতে যে পরিমাণ কার্য করতে হয়, তাকে ওই দুই বিন্দুর বিভব পার্থক্য বা বিভব প্রভেদ বলে।
বিভব প্রভেদের একক ও মাত্রা:
CGS পদ্ধতিতে বিভব প্রভেদের একক হল: esu of potential বা স্ট্যাটভোল্ট
SI পদ্ধতিতে বিভব প্রভেদের একক হল: ভোল্ট (volt)
তড়িৎচ্চালক বলের ধারণা (Concept of Electromotive Force):
কোনও নলের মধ্য দিয়ে জলপ্রবাহের জন্য যেমন বাইরে থেকে একটি বল প্রয়োগ করতে হয় বা কোনও বস্তুকে গতিশীল করার জন্য যেমন একটি বলের প্রয়োজন তেমনই কোনো পরিবাহীর মধ্য দিয়ে আধানের প্রবাহ বজায় রাখার জন্য একটি বলের প্রয়োজন। যখন কোনও সংস্থা (তড়িৎকোশ বা ডায়নামো) তড়িৎ বর্তনীতে আধানের প্রবাহকে বজায় রাখে তখন আমরা একটি বল কল্পনা করতে পারি, যা সংস্থার অভ্যন্তরে ধনাত্বক আধানকে নিম্নতর বিভবের প্রান্ত থেকে (ঋনাত্বক তড়িৎদ্বার) থেকে উচ্চতর বিভবের প্রান্তে (ধনাত্বক তড়িৎদ্বারে) নিয়ে যায়। সংস্থার অভ্যন্তরে এই ধনাত্বক আধানের উপর প্রযুক্ত ওই বলের জন্য বর্তনীতে আধানের প্রবাহ বজায় থাকে। এই বলই হল তড়িৎচ্চালক বল। একে emf বলে।
বর্তনীর অন্য অংশে ধনাত্বক আধান যথারীতি উচ্চতর বিভবের প্রান্ত থেকে নিম্নতর বিভবের প্রান্তে যায়। কিন্তু তড়িৎকোশ বা ডায়নামোর এই বল এবং গতিবিদ্যার (Mechanics) বল সম্পূর্ণ আলাদা জিনিস। তড়িতচ্চালক বল আসলে কোনও বল নয়। এই তড়িৎচ্চালক বলের সঙ্গে সাধারণ বলের কোনও মিল নেই। এটি একটি রূপান্তরিত শক্তি যা বর্তনীর প্রবাহ বজায় রাখার জন্য কৃতকার্যের সমান হয়। তড়িৎকোশ, ডায়নামো ইত্যাদি যন্ত্র কোনও বাহ্যিক শক্তিকে তড়িৎ শক্তিতে রূপান্তরিত করে, তখন তড়িৎচ্চালক বলের সৃষ্টি হয়। তাই তড়িৎকোশ এমন একটি ব্যবস্থা যেখানে কোনও যন্ত্রের সাহায্য ছাড়াই অন্য কোনও শক্তিকে তড়িৎশক্তিতে রূপান্তরিত করা যায়। তড়িৎকোশে সাধারণত রাসায়নিক শক্তি তড়িৎশক্তিতে রূপান্তরিত হয়।
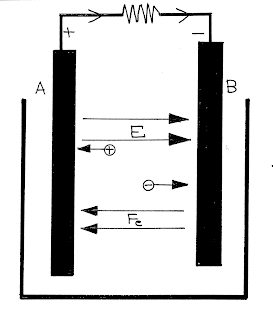 |
| তড়িৎকোশের তড়িৎচ্চালক বল |
একটি তড়িৎকোশে দুটি ধাতব পাত \(A\) এবং \(B\), একটি রাসায়নিক দ্রবনে আংশিকভাবে ডোবানো রয়েছে। এখানে ধনাত্বক আধানযুক্ত \(A\) পাতে উচ্চবিভব এবং ঋনাত্বক আধানযুক্ত \(B\) পাতে একটি নিম্ন বিভবের সৃষ্টি হয়। ফলে \(A\) পাত থেকে \(B\) পাতের দিকে একটি তড়িৎক্ষেত্র \(E\) সৃষ্টি হয়। এখন কোশটির অভ্যন্তরে অবস্থিত একটি \(q\) আধানের উপর \(\overrightarrow {{F_e}} = q\overrightarrow E \) বল \(A\) পাত থেকে \(B\) পাতের দিকে ক্রিয়া করে।
আবার কোশের মধ্যে রাসায়নিক বিক্রিয়ার ফলে একপ্রকার কোশীয় বলের (Cell force) উদ্ভব হয় যার প্রকৃতি স্থির তাড়িতিক (non-electrostatic) নয়। \(q\) আধানের উপর এই কোশীয় বল (\(\overrightarrow {{F_C}} \)) ক্রিয়া করে যা আধানটিকে \(B\) পাত থেকে \(A\) পাতের দিকে নিয়ে যায়।
সাম্যাবস্থায় \(A\) এবং \(B\) পাতে এমন পরিমান আধান জমা হয় যে, \({\overrightarrow F _e} = {\overrightarrow F _C}\) হয় এবং আর আধান জমা হয় না।
এই অবস্থায় \(q\) আধানকে \(B\) পাত থেকে \(A\) পাতে নিয়ে গেলে কোশীয় বল দ্বারা কৃতকার্য হয়
\(W = {\overrightarrow F _C} \times d\), যেখানে \(d\) হল পাতদুটির মধ্যবর্তী ব্যবধান। এখন একক আধানের জন্য কৃতকার্য হয় \( = {W_1} = \frac{{{{\overrightarrow F }_C} \times d}}{q}\)। একেই কোশের তড়িৎচ্চালক বলে।
এখন \(A\) এবং \(B\) পাতকে বাইরে থেকে পরিবাহী তার দ্বারা যোগ না করা হলে \({F_C} = {F_E} = \frac{{{F_c} \times d}}{q} = \frac{{qEd}}{q} = Ed = V\) হয়। সুতরাং একটি কোশ যখন বহিঃবর্তনীতে কোনও তড়িৎপ্রবাহ না পাঠায় তখন তার দুটির মধ্যে যে বিভব পার্থক্যের সৃষ্টি হয় তাকে ওই কোশের তড়িৎচ্চালক বলে।
এখন, কোশের তড়িৎদ্বার দুটিকে (A, B) কোনও পরিবাহী তার দ্বারা যোগ করলে \(B\) পাত থেকে ইলেকট্রন \(A\) পাতে যায়। ফলে \(A\) ও \(B\) পাতের মধ্যে বিভব প্রভেদ কমে। তার ফলে কোশের অভ্যন্তরে \(q\) আধানের উপর কার্যকরী স্থির তাড়িতিক বল \({\overrightarrow F _e}\) এর মান কমতে থাকে। কিন্তু কোশের অভ্যন্তরে কোশীয় বল \({\overrightarrow F _C}\) একই থাকে। ফলে \(q\) আধানের উপর একটি লব্ধি বল ক্রিয়া করে যা \(q\) আধানটিকে কোশের অভ্যন্তরে \(B\) পাত থেকে \(A\) পাতে নিয়ে আসে। এর ফলে \(A\) এবং \(B\) পাতের মধ্যে বিভব পার্থক্য বজায় থাকে এবং বহিঃবর্তনীতে একটি তড়িৎ প্রবাহ পাওয়া যায়।
এই ধনাত্বক আধানকে কোশের অব্যন্তরে ঋনাত্বক তড়িৎদ্বার থেকে ধনাত্বক তড়িৎদ্বারে নিয়ে যেতে যে শক্তির প্রয়োজন তা নির্ভর করে কোশে ব্যবহৃত সক্রিয় তরলের রাসায়নিক প্রকৃতি এবং ব্যবহৃত তড়িৎদ্বারের উপর। কোশের আকারের উপর নয়।
তড়িৎচ্চালক বলের সংজ্ঞা (Definition of EMF):
মুক্ত বর্তনীতে কোনও তড়িৎকোশের দুটি মেরুর মধ্যে যে বিভব পার্থক্য থাকে, তাকে ওই কোশের তড়িৎচ্চালক বল বলে। বা
মুক্ত বর্তনীতে কোনও তড়িৎকোশের অভ্যন্তরে একক ধনাত্বক আধানকে নিম্নবিভবের পাত থেকে উচ্চবিভবের পাতে নিয়ে যেতে যে পরিমান কার্য সম্পাদন করতে হয়, তাকে ওই কোশের তড়িৎচ্চালক বল বলে।
তড়িৎউৎসের মধ্য দিয়ে নিম্ন বিভব থেকে উচ্চবিভবে একক ধনাত্বক আধানকে স্থানান্তরান করার জন্য সম্পাদিত কৃতকার্যের পরিনমান কে োই উৎসের তড়িৎচ্চালক বল বলে।
তাই তড়িৎচ্চালক বল = সম্পাদিত কৃতকার্য/স্থানান্তরিত তড়িতাধানের পরিমান = তড়িৎশক্তি/স্থানান্তরিত তড়িতাধান
কোশের তড়িৎচ্চালক বল:
কোনও কোশ যুক্ত পূর্ণ বর্তনীতে (বহিঃবর্তনী ও কোশের মধ্য দিয়ে) একক ধনাত্বক মানের আধানকে একবার আবর্তন করাতে যে পরিমান কার্য করতে হয়, তাকে ওই কোশটির তড়িৎচ্চালক বল বলে। অর্থাৎ মুক্ত বর্তনীতে কোনও তড়িৎকোশের দুটি মেরুর মধ্যে যে বিভব পার্থক্য থাকে তাকে ওই কোশের তড়িৎচ্চালক বল বলে।
যেমন, একটি কোশের তড়িৎচ্চালক বল \(1.5V\) বলতে বোঝায় যে, ওই কোশ যুক্ত পূর্ণ বর্তনীতে \(1\) কুলম্ব তড়িতাধানকে একবার সম্পূর্ণ আবর্তন করাতে \(1.5\) জুল কার্য করতে হয়। অর্থাৎ মুক্ত বর্তনীতে ওই কোশটির দুটি মেরুর মধ্যে \(1.5\) ভোল্ট বিভব পার্থক্য থাকে।
কোশের বিভব পার্থক্য:
কোনও কোশের বহিঃবর্তনী বরাবর একক তড়িতাধানকে একটি তড়িৎদ্বার থেকে অপর তড়িৎদ্বারে নিয়ে যেতে যে পরিমান কার্য করতে হয় তাকে ওই কোশটির বিভব প্রভেদ বলে। অর্থাৎ বদ্ধ বর্তনীতে কোশের দুটি মেরুর মধ্যে যে বিভব পার্থক্য থাকে তাকে ওই কোশের বিভব প্রভেদ বলে।
যেমন, কোনও কোশের বিভব প্রভেদ \(1.4V\) বলতে বোঝায় যে, বদ্ধ বর্তনীতে ওই কোশটির দুটি মেরুর মধ্যে \(1.4V\) বিভব পার্থক্য থাকে।
তড়িৎচ্চালক বলের একক:
SI পদ্ধতিতে তড়িৎচ্চালক বলের একক হল: ভোল্ট
কয়েকটি বহুল ব্যবহৃতা কোশের তড়িৎচ্চালক বলের মান নিম্নে দেওয়া হল:
বল ও তড়িৎচ্চালক বল হল ভিন্ন রাশি:
গতিবিদ্যায় বল = কৃতকার্য/সরণ
কিন্তু কোনও তড়িৎকোশের তড়িৎচ্চালক বল হল = তড়িৎশক্তির পরিমান/স্থানান্তরিত তড়িতাধান
এদের মধ্যে কার্য ও তড়িৎশক্তি একই রাশি। এদের একক ও মাত্রা একই। কিন্তু সরণ ও তড়িতাধান সম্পূর্ণ ভিন্ন ভৌতরাশি তাই, গতিবিজ্ঞানে বল (Force) এবং চলতড়িতের কোশের তড়িৎচ্চালক বল (Electromotive Force) সম্পূর্ণ পৃথক রাশি।
তড়িৎপ্রবাহের ধারণা (Concept of Electric Current):
কোনও পরিবাহীর মধ্যে তড়িৎগ্রস্থ কণার প্রবাহকে তড়িৎপ্রবাহ বলে। পরিবাহীর যেকোনও প্রস্থচ্ছেদের মধ্য দিয়ে একক সময়ে যে পরিমাণ তড়িৎগ্রস্থ কণা প্রবাহিত হয়, তাই হল তড়িৎপ্রবাহের পরিমান বা তড়িৎপ্রবাহমাত্রা।
কোনও পরিবাহীর দুই প্রান্তে বিভবের পার্থক্য থাকলে উচ্চ বিভবের প্রান্ত থেকে নিম্ন বিভবের দিকে তড়িৎ প্রবাহিত হয়।
ধাতব পরিবাহীতে মুক্ত ইলেকট্রন গুলি তড়িৎ পরিবহনে অংশগ্রহন করে। এবং মুক্ত ইলেকট্রনগুলি ঋনাত্বক কণিকা হওয়ায় এদের গতি নিম্ন বিভব থেকে উচ্চ বিভবের দিকে। কিন্তু তড়িৎপ্রবাহের অভিমুখ বলতে ধনাত্বক আধানের গতিকে নির্দেশ করে তাই তড়িৎপ্রবাহ বলতে কোনও পরিবাহীতে মুক্ত ইলেকট্রনের গতির বিপরীত দিককে ধরা হয়।
তড়িৎপ্রবাহমাত্রা:
পরিবাহীর যেকোনও প্রস্থচ্ছেদের মধ্য দিয়ে প্রতি একক সময়ে যে পরিমাণ তড়িতাধান প্রবাহিত হয়, তাকে ওই পরিবাহীতে তড়িৎপ্রবাহমাত্রা বলে। অর্থাৎ কোনও পরিবাহীতে সময়ের সাপেক্ষে তড়িতাধানের প্রবাহের হারকে তড়িৎপ্রবাহমাত্রা বলে।
যদি কোনও পরিবাহীর (যেকোনো প্রস্থচ্ছেদের) মধ্য দিয়ে \(t\) সময়ে \(Q\) পরিমাণ তড়িতাধান প্রবাহিত হয় তাহলে ওই পরিবাহীতে তড়িৎপ্রবাহমাত্রা,
\(I = \frac{Q}{t}\) = তড়িতাধান/সময়
বা, \(Q = It\)
তড়িৎপ্রবাহমাত্রার একক ও মাত্রা:
আমরা প্রবাহমাত্রার সংজ্ঞা থেকে পাই \(I = \frac{Q}{t}\)
SI পদ্ধতিতে তড়িতাধানকে একক কুলম্ব এবং সময়ের একক সেকেন্ড।
তাই SI পদ্ধতিতে প্রবাহমাত্রার একক = কুলম্ব/সময় = অ্যাম্পিয়ার
\(1A = \frac{{1C}}{{1s}}\)
তাই বলা যায়, যেকোনও প্রস্থচ্ছেদের পরিবাহীর মধ্য দিয়ে এক সেকেন্ড সময়ে এক কুলম্ব তড়িতাধান প্রবাহিত হলে, ওই পরিবাহীর প্রবাহমাত্রা হয় এক অ্যাম্পিয়ার।
CGS পদ্ধতিতে তড়িৎপ্রবাহমাত্রার একক হল: স্ট্যাট অ্যাম্পিয়ার।
CGS ও SI পদ্ধতিতে প্রবাহমাত্রার এককের মধ্যে সম্পর্ক:
\(1A = \frac{{1C}}{{1s}} = \frac{{3 \times {{10}^9}esu}}{{1s}} = 3 \times {10^9}stat - ampere\)
প্রবাহমাত্রা কিছু ছোটো ও বড় একক:
\(1mA = {10^{ - 3}}A\)
\(1\mu A = {10^{ - 6}}A\)
তড়িৎচ্চালক বল ও বিভবপ্রভেদের পার্থক্য:
কোশের তড়িৎচ্চালক বল:
কোনও কোশ যুক্ত পূর্ণ বর্তনীতে (বহিঃবর্তনী ও কোশের মধ্য দিয়ে) একক ধনাত্বক মানের আধানকে একবার আবর্তন করাতে যে পরিমান কার্য করতে হয়, তাকে ওই কোশটির তড়িৎচ্চালক বল বলে। অর্থাৎ মুক্ত বর্তনীতে কোনও তড়িৎকোশের দুটি মেরুর মধ্যে যে বিভব পার্থক্য থাকে তাকে ওই কোশের তড়িৎচ্চালক বল বলে।
যেমন, একটি কোশের তড়িৎচ্চালক বল \(1.5V\) বলতে বোঝায় যে, ওই কোশ যুক্ত পূর্ণ বর্তনীতে \(1\) কুলম্ব তড়িতাধানকে একবার সম্পূর্ণ আবর্তন করাতে \(1.5\) জুল কার্য করতে হয়। অর্থাৎ মুক্ত বর্তনীতে ওই কোশটির দুটি মেরুর মধ্যে \(1.5\) ভোল্ট বিভব পার্থক্য থাকে।
কোশের বিভব পার্থক্য:
কোনও কোশের বহিঃবর্তনী বরাবর একক তড়িতাধানকে একটি তড়িৎদ্বার থেকে অপর তড়িৎদ্বারে নিয়ে যেতে যে পরিমান কার্য করতে হয় তাকে ওই কোশটির বিভব প্রভেদ বলে। অর্থাৎ বদ্ধ বর্তনীতে কোশের দুটি মেরুর মধ্যে যে বিভব পার্থক্য থাকে তাকে ওই কোশের বিভব প্রভেদ বলে।
যেমন, কোনও কোশের বিভব প্রভেদ \(1.4V\) বলতে বোঝায় যে, বদ্ধ বর্তনীতে ওই কোশটির দুটি মেরুর মধ্যে \(1.4V\) বিভব পার্থক্য থাকে।
তড়িৎচ্চালক বলের একক:
SI পদ্ধতিতে তড়িৎচ্চালক বলের একক হল: ভোল্ট
কয়েকটি বহুল ব্যবহৃতা কোশের তড়িৎচ্চালক বলের মান নিম্নে দেওয়া হল:
| ক্রমিক সংখ্যা | কোশের নাম | তড়িৎচ্চালক বলের নাম |
|---|---|---|
| 1 | সরল ভোল্টীয় কোশ | 1.08 volt |
| 2 | লেকল্যান্স কোশ | 1.5 volt |
| 3 | ড্যানিয়েল কোশ | 1.08 volt |
| 4 | সঞ্চয়ক কোশ | 2.1 volt |
বল ও তড়িৎচ্চালক বল হল ভিন্ন রাশি:
গতিবিদ্যায় বল = কৃতকার্য/সরণ
কিন্তু কোনও তড়িৎকোশের তড়িৎচ্চালক বল হল = তড়িৎশক্তির পরিমান/স্থানান্তরিত তড়িতাধান
এদের মধ্যে কার্য ও তড়িৎশক্তি একই রাশি। এদের একক ও মাত্রা একই। কিন্তু সরণ ও তড়িতাধান সম্পূর্ণ ভিন্ন ভৌতরাশি তাই, গতিবিজ্ঞানে বল (Force) এবং চলতড়িতের কোশের তড়িৎচ্চালক বল (Electromotive Force) সম্পূর্ণ পৃথক রাশি।
তড়িৎপ্রবাহের ধারণা (Concept of Electric Current):
কোনও পরিবাহীর মধ্যে তড়িৎগ্রস্থ কণার প্রবাহকে তড়িৎপ্রবাহ বলে। পরিবাহীর যেকোনও প্রস্থচ্ছেদের মধ্য দিয়ে একক সময়ে যে পরিমাণ তড়িৎগ্রস্থ কণা প্রবাহিত হয়, তাই হল তড়িৎপ্রবাহের পরিমান বা তড়িৎপ্রবাহমাত্রা।
 |
| তড়িৎপ্রবাহমাত্রা |
ধাতব পরিবাহীতে মুক্ত ইলেকট্রন গুলি তড়িৎ পরিবহনে অংশগ্রহন করে। এবং মুক্ত ইলেকট্রনগুলি ঋনাত্বক কণিকা হওয়ায় এদের গতি নিম্ন বিভব থেকে উচ্চ বিভবের দিকে। কিন্তু তড়িৎপ্রবাহের অভিমুখ বলতে ধনাত্বক আধানের গতিকে নির্দেশ করে তাই তড়িৎপ্রবাহ বলতে কোনও পরিবাহীতে মুক্ত ইলেকট্রনের গতির বিপরীত দিককে ধরা হয়।
তড়িৎপ্রবাহমাত্রা:
পরিবাহীর যেকোনও প্রস্থচ্ছেদের মধ্য দিয়ে প্রতি একক সময়ে যে পরিমাণ তড়িতাধান প্রবাহিত হয়, তাকে ওই পরিবাহীতে তড়িৎপ্রবাহমাত্রা বলে। অর্থাৎ কোনও পরিবাহীতে সময়ের সাপেক্ষে তড়িতাধানের প্রবাহের হারকে তড়িৎপ্রবাহমাত্রা বলে।
যদি কোনও পরিবাহীর (যেকোনো প্রস্থচ্ছেদের) মধ্য দিয়ে \(t\) সময়ে \(Q\) পরিমাণ তড়িতাধান প্রবাহিত হয় তাহলে ওই পরিবাহীতে তড়িৎপ্রবাহমাত্রা,
\(I = \frac{Q}{t}\) = তড়িতাধান/সময়
বা, \(Q = It\)
তড়িৎপ্রবাহমাত্রার একক ও মাত্রা:
আমরা প্রবাহমাত্রার সংজ্ঞা থেকে পাই \(I = \frac{Q}{t}\)
SI পদ্ধতিতে তড়িতাধানকে একক কুলম্ব এবং সময়ের একক সেকেন্ড।
তাই SI পদ্ধতিতে প্রবাহমাত্রার একক = কুলম্ব/সময় = অ্যাম্পিয়ার
\(1A = \frac{{1C}}{{1s}}\)
তাই বলা যায়, যেকোনও প্রস্থচ্ছেদের পরিবাহীর মধ্য দিয়ে এক সেকেন্ড সময়ে এক কুলম্ব তড়িতাধান প্রবাহিত হলে, ওই পরিবাহীর প্রবাহমাত্রা হয় এক অ্যাম্পিয়ার।
CGS পদ্ধতিতে তড়িৎপ্রবাহমাত্রার একক হল: স্ট্যাট অ্যাম্পিয়ার।
CGS ও SI পদ্ধতিতে প্রবাহমাত্রার এককের মধ্যে সম্পর্ক:
\(1A = \frac{{1C}}{{1s}} = \frac{{3 \times {{10}^9}esu}}{{1s}} = 3 \times {10^9}stat - ampere\)
প্রবাহমাত্রা কিছু ছোটো ও বড় একক:
\(1mA = {10^{ - 3}}A\)
\(1\mu A = {10^{ - 6}}A\)
তড়িৎচ্চালক বল ও বিভবপ্রভেদের পার্থক্য:
| তড়িৎচ্চালক বল | বিভব পার্থক্য |
|---|---|
| (1) তড়িৎ বর্তনীর যে অংশে অন্য কোনো শক্তি তড়িৎশক্তিতে রূপান্তরিত হয়, সেখানে তড়িৎচ্চালক বলের সৃষ্টি হয়। | (1) তড়িৎবর্তনীর যে অংশে তড়িৎশক্তি অন্য কোনো শক্তিতে রূপান্তরিত হয়, সেখানে বিভব প্রভেদ সৃষ্টি হয়। |
| (2) মুক্ত বর্তনীতে তড়িৎকোশের দুই মেরুর মধ্যে যে বিভবের পার্থক্য থাকে, তাই হল কোশের তড়িৎচ্চালক বল। | (2) বদ্ধ বর্তনীতে তড়িৎকোশের দুই মেরুর মধ্যে যে বিভবের পার্থক্য থাকে, তাকে বিভব প্রভেদ বলে। |
| (3) তড়িৎচ্চালক বল হল বিভবপ্রভেদের কারণ। | (3) বিভব প্রভেদ হল তড়িৎচ্চালক বলের ফল। |
| (4) তড়িৎচ্চালক বল পোটেনশিওমিটার যন্ত্রের সাহায্যে পরিমাপ করা হয়। | (4) বিভব প্রভেদ ভোল্টমিটার যন্ত্রের সাহায্যে পরিমাপ করা হয়। |




![[feature] current electricity current electricity](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEgBIpgtnZOr3AGd11jQ-1x2I5BaRDfYrvbqIHhb3BAKxv2jF19f2ZmOaRb32ZgPphTmi7pW7St1B1wdfoig7gmTrYK6a0cZCTO-pb7_TydAMl12PxF-_FIRFOR2rYrdOdrxn6SRUfVbS3u9/s200/2000px-Current_notation.svg.png)










COMMENTS