Tips and Tricks to solve the Mechanics Problem using Free Body Diagram Part: 1

Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situati...

Free-body diagrams are diagrams used to show the relative magnitude and direction of all forces acting upon an object in a given situation. A free-body diagram is a special example of the vector diagrams that were discussed in an earlier unit. The drawing of a free-body diagram is an important step in the solving of mechanics problems since it helps to visualize all the forces acting on a single object. The net external force acting on the object must be obtained in order to apply Newton's Second Law to the motion of the object.

In physics a free body diagram (force diagram or FBD) is a graphical illustration used to visualize the applied forces, movements, and resulting reactions on a body in a steady state condition (no acceleration of the system). They depict a body or connected bodies with all of the applied forces and moments, as well as reactions, that act on that/those bodies. The body may consist of multiple internal members, for example, a truss, or be a compact body such as a beam. A series of free bodies and other diagrams may be necessary to solve complex problems.

Free body diagrams are used to visualize the forces and moments applied to a body and calculate the resulting reactions, in many types of mechanics problems. Most free body diagrams are used both to determine the loading of individual structural components as well as calculating internal forces within the structure in almost all engineering disciplines from Biomechanics to Structural. In the educational environment, learning to draw a free body diagram is an important step in understanding certain topics in physics, such as statics, dynamics and other forms of classical mechanics. One professor at Cornell University earned the nickname "Free-Body Perkins" because of his passion for teaching the importance of using free body diagrams to solve mechanics problems. He went so far as to stop random students in the hall, saying, “You! Come in my office! Draw a free body diagram.

A block rests on a horizontal surface:

(1) A block rests on a friction-less horizontal surface and the block pulled horizontally with a force \(F\).

Block Rest on Horizontal Surface

From free body diagram we get, \(R = mg\) and from Newton's law \(F = ma\)

Thus, \(a = \frac{F}{m}\)

(2) A block rests on a horizontal surface where co-efficient of friction between the block and the surface is \(\mu \) and the block pulled horizontally with a force \(F\):

Block rest on Horizontal Surface

From free body diagram we get, \(R = mg\) and from Newton's law \(F - f = ma\)

or, Acceleration \(a = \frac{{F - f}}{m} = \frac{{F - \mu R}}{m} = \frac{{F - \mu mg}}{m}\)

(3) A block rests on a horizontal surface and a pull is acting at an angle \(\theta \) to the horizontal in upward direction:

Block Rest on Horizontal Surface

From free body diagram we get, \(R + F\sin \theta  = mg\)

or, \(R = mg - F\sin \theta \)

And the net effective force on the block along horizontal direction is \(F\cos \theta \), Thus from Newton's law we get, \(ma = F\cos \theta \)

or, Acceleration \(a = \frac{{F\cos \theta }}{m}\)

(4) A block rests on a horizontal plane and a pushing force \(F\) acts downward direction at an angle \(\theta \) to the horizontal:

Block Rest on Horizontal Surface

From free body diagram we get, \(R = mg + F\sin \theta \)

And the net effective force of the block along horizontal direction is \(F\cos \theta \)

Thus from Newton's law we get, \(ma = F\cos \theta \)

or, Acceleration \(a = \frac{{F\cos \theta }}{m}\)

Motion of a Block on Inclined Plane:

(1) A block placed on a friction-less inclined plane with angle of inclination \(\theta \). Here the inclined plane is at rest and the body slides down the inclined plane.

Block Rest on Inclined Plane

From free body diagram we get, \(R = mg\cos \theta \), and the net effective force on the block is \(F = mg\sin \theta \). From Newton's law we get, \(F = ma\)

Therefore, \(ma = mg\sin \theta \)

or, \(a = g\sin \theta \)

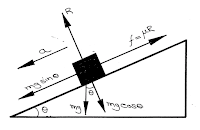
(2) A block placed on a inclined plane with angle of inclination \(\theta \) and whose co-efficient of friction between the surface of the block and the inclined plane is \(\mu \). Here the inclined plane is at rest and the body slides down the inclined plane:

Block Rest on Inclined Plane

From free body diagram we get, \(R = mg\cos \theta \) and the friction force \(f = \mu R = \mu mg\cos \theta \) act upward opposes the downward motion. And the net effective force on the block is \(F = mg\sin \theta  - \mu mg\cos \theta \).

Thus from Newton's law we get \(F = ma\)

Therefore, \(ma = mg\sin \theta  - \mu mg\cos \theta \)

or, \(a = g\sin \theta  - \mu g\cos \theta \)

or, \(a = g\left( {\sin \theta  - \mu \cos \theta } \right)\)

(3) Retardation of a block upward in a rough inclined plane:

Block Rest on Inclined Plane

From free body diagram we get, \(R = mg\cos \theta \), Here friction force \(f = \mu R = \mu mg\cos \theta \) acts downward opposes the upward motion of the block. And the net effective force on the block is \(F = mg\sin \theta  + \mu mg\cos \theta \)

Thus from Newton's law of motion we get, \(F = ma\)

or, \(ma = mg\sin \theta  + \mu mg\cos \theta \)

or, \(a = g\sin \theta  + \mu g\cos \theta \)

or, Acceleration \(a = g\left( {\sin \theta  + \mu \cos \theta } \right)\)

(4) A block placed on a friction-less inclined plane with angle of inclination \(\theta \). Here the inclined plane is in an acceleration \(b\) and the body slides down the inclined plane.

Block Rest on Inclined Plane

Block Rest on Inclined Plane

Since the body lie in ARF (Accelerated reference frame), an inertial force \(mb\) acts on it's in the opposite direction. From free body diagram we get, \(R = mg\cos \theta  + mb\sin \theta \),.

And the net effective force on the block is \(F = mg\sin \theta  - mb\cos \theta \). From Newton's law of motion we get, \(F = ma\)

Therefore, \(ma = mg\sin \theta  - mbcos\theta \)

or, \(a = g\left( {\sin \theta  - b\cos \theta } \right)\)

Special Notes: The condition for the body to be rest relative to the inclined plane if \(a = 0\)

Thus, \(g\sin \theta  - b\cos \theta  = 0\)

or, \(b\cos \theta  = gsin\theta \)

or, \(b = g\tan \theta \)

Motion of a Block in Contact:

(1) Two body in contact and force apply on the left side of the block:

Two Body System in Contact

FBD of First Block

FBD of Second Block

Here \(F\) be the applied force on \({m_1}\) and \(f\) be the contact force between \({m_1}\) and \({m_2}\), then from free body diagram we get,

For mass \({m_1}\):

\(F - f = {m_1}a\)

For mass \({m_2}\):

\(f = {m_2}a\)

From these two equation we get, 

\(F - {m_2}a = {m_1}a\)

or, \(\left( {{m_1} + {m_2}} \right)a = F\)

or, \(a = \frac{F}{{\left( {{m_1} + {m_2}} \right)}}\)

And contact force \(f = {m_2}a = \frac{{{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}F\)

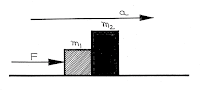
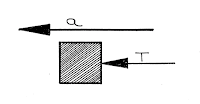
(2) Two body in contact and a force apply on the right side of the block:

Two Body System in Contact

FBD of First Block

FBD of Second Block

Here \(F\) be the applied force on \({m_2}\) and \(f\) be the contact force between \({m_1}\) and \({m_2}\), then from free body diagram we get

For mass \({m_2}\):

\(F - f = {m_2}a\)

For mass \({m_1}\):

\(f = {m_1}a\)

From these two equation we get, \(F - {m_1}a = {m_2}a\)

or, \(\left( {{m_1} + {m_2}} \right)a = F\)

or, \(a = \frac{F}{{\left( {{m_1} + {m_2}} \right)}}\)

And the contact force \(f = {m_1}a = \frac{{{m_1}}}{{\left( {{m_1} + {m_2}} \right)}}F\)

(3) Three body in contact and force apply to the left side of the block:

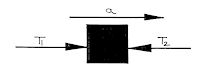
Three Body in Contact

FBD of First Body

FBD of Second Body

FBD of Third Body

 Here \(F\) is the applied force on \({m_1}\) and \({f_{12}}\) be the contact force between the bodies of masses \({m_1}\) and \({m_2}\) and \({f_{23}}\) be the contact force between the bodies of masses \({m_2}\) and \({m_3}\), then from free body diagram we get,
For mass \({m_1}\):
\(F - {f_{12}} = {m_1}a\)
For mass \({m_2}\):
\({f_{12}} - {f_{23}} = {m_2}a\)
For mass \({m_3}\):
\({f_{23}} = {m_3}a\)
From these three equation we get,
\({f_{12}} - {m_3}a = {m_2}a\)
or, \({f_{12}} = \left( {{m_2} + {m_3}} \right)a\)
So, \(F - \left( {{m_2} + {m_3}} \right)a = {m_1}a\)
or, \(F = \left( {{m_1} + {m_2} + {m_3}} \right)a\)
or, \(a = \frac{F}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}\)
And the contact force between the masses \({m_2}\) and \({m_3}\) is \({f_{23}} = \frac{{{m_3}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\) And the contact force between \({m_1}\) and \({m_2}\) is \({f_{12}} = \left( {{m_2} + {m_3}} \right)a = \frac{{\left( {{m_2} + {m_3}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\)

(4) Three body in contact and a force apply on the right side of the block:

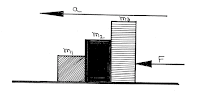Three Body in Contact

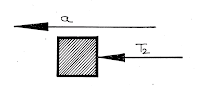FBD of First Body

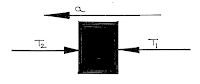FBD of Second Body

FBD of Third Body

  

Here \(F\) is the applied force on \({m_3}\) and \({f_{12}}\) be the contact force between the bodies of masses \({m_1}\) and \({m_2}\) and \({f_{23}}\) be the contact force between the bodies on masses \({m_2}\) and \({m_3}\), then from free body diagram we get,
For mass \({m_1}\):
\({f_{12}} = {m_1}a\)
For mass \({m_2}\):
\({f_{23}} - {f_{12}} = {m_2}a\)
For mass \({m_3}\):
\(F - {f_{23}} = {m_3}a\)
From these three equation we get,
\({f_{23}} - {m_1}a = {m_2}a\)
or, \({f_{23}} = \left( {{m_1} + {m_2}} \right)a\)
So, \(F - \left( {{m_1} + {m_2}} \right)a = {m_3}a\)
or, \(F = \left( {{m_1} + {m_2} + {m_3}} \right)a\)
or, \(a = \frac{F}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}\)
And contact force between the masses \({m_1}\) and \({m_2}\) is \({f_{12}} = \frac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}a\) and the contact force between \({m_2}\) and \({m_3}\) is \({f_{23}} = \left( {{m_1} + {m_2}} \right)a = \frac{{\left( {{m_1} + {m_2}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\)

(5) Four body in contact:

Four Body System in Contact

Let A, B, C and D four body of masses \({m_1}\), \({m_2}\), \({m_3}\) and \({m_4}\) are in contact. Now the force \(F\) is applied on mass \({m_4}\). Here Acceleration of the system will be \(a = \frac{F}{{\left( {{m_1} + {m_2} + {m_3} + {m_4}} \right)}}\)
And contact force between mass \({m_1}\) and \({m_2}\) is \(\frac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3} + {m_4}} \right)}}F\), the contact force between \({m_2}\) and \({m_3}\) is \(\frac{{\left( {{m_1} + {m_2}} \right)}}{{\left( {{m_1} + {m_2} + {m_3} + {m_4}} \right)}}F\), and the contact force between \({m_3}\) and \({m_4}\) is \(\frac{{\left( {{m_1} + {m_2} + {m_3}} \right)}}{{\left( {{m_1} + {m_2} + {m_3} + {m_4}} \right)}}F\)

Motion of a Block connected in mass-less string:

(1) Two body system and a pulling force acts on the right side:

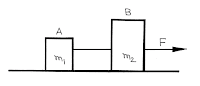Two Body System

FBD of First Body

FBD of Second Body

Let A and B the two body of masses \({m_1}\) and \({m_2}\) are connected by a mass-less string and a pulling force F is applied on the body A. If the tension of the string between the two body is T then, from free body diagram,
For body \({m_1}\):
\(F - T = {m_1}a\)
For body \({m_2}\):
\(T = {m_2}a\)
From these two equation we get,
\(F - {m_2}a = {m_1}a\)
or, \(\left( {{m_1} + {m_2}} \right)a = F\)
or, \(a = \frac{F}{{\left( {{m_1} + {m_2}} \right)}}\)
And, the tension of the string between the mass \({m_1}\) and \({m_2}\) is \[T = {m_2}a = \frac{{{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}F\]

(2) Two body system and a pulling force acts on the left side:

Two Body System

FBD of First Body

FBD of Second Body

Let A and B the two body of masses \({m_1}\) and \({m_2}\) are connected by a mass-less string and a pulling force F is applied on the body \({m_1}\). If the tension of the string between the two body is T then, from free body diagram,
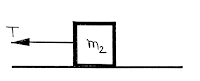
For body \({m_1}\):
\(F - T = {m_1}a\)
For body \({m_2}\):
 \(T = {m_2}a\)
From these two equation we get, \(F - {m_2}a = {m_1}a\)
or, \(F = \left( {{m_1} + {m_2}} \right)a\)
or, \(a = \frac{F}{{\left( {{m_1} + {m_2}} \right)}}\)
And the tension of the string between he mass \({m_1}\) and \({m_2}\) is \(T = {m_2}a = \frac{{{m_2}}}{{\left( {{m_1} + {m_2}} \right)}}F\)

(3) Three body system and a pulling force acts on the right side:

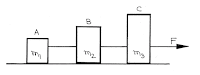Three Body System

FBD of First Body

FBD of Second Body

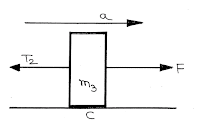FBD of Third Body

Let A, B and C be the three body of masses \({m_1}\), \({m_2}\) and \({m_3}\) are connected by a mass-less string and a pulling force \(F\) is applied on a body C. If tension of the string between \({m_2}\) and \({m_3}\) is \({T_{23}}\) and the tension of the string between the body \({m_1}\) and \({m_2}\) is \({T_{12}}\) then, from free body diagram we get,
For body of mass \({m_1}\):
\({T_{12}} = {m_1}a\)
For body of mass \({m_2}\):
\({T_{23}} - {T_{12}} = {m_2}a\)
For body of mass \({m_3}\):
\(F - {T_{23}} = {m_3}a\)
From these three equation we get,
\({T_{23}} - {m_1}a = {m_2}a\)
or, \({T_{23}} = \left( {{m_1} + {m_2}} \right)a\)
And, \(F - \left( {{m_1} + {m_2}} \right)a = {m_3}a\)
or, \(F = \left( {{m_1} + {m_2} + {m_3}} \right)a\)
or, \(a = \frac{F}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}\)
And the tension of the string between the mass \({m_1}\) and \({m_2}\) is \({T_{12}} = {m_1}a = \frac{{{m_1}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\), And the tension of the string between he mass \({m_2}\) and \({m_3}\) is \({T_{23}} = \left( {{m_1} + {m_2}} \right)a = \frac{{\left( {{m_1} + {m_2}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\)

(4) Three body system and a pulling force acts on the left side:

Three Body System

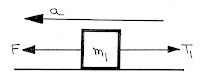FBD of First Body

FBD of Second Body

FBD of Third Body

Let A, B and C is the three bodies of masses \({m_1}\), \({m_2}\) and \({m_3}\) are connected by a mass-less string and a pulling force \(F\) is applied on a body A. If the tension of the string between \({m_2}\) and \({m_3}\) is \({T_2}\) and the tension of the string between the body of masses \({m_1}\) and \({m_2}\) is \({T_1}\) then, from free body diagram we get
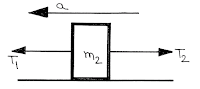
For body of mass \({m_1}\);
\(F - {T_1} = {m_1}a\)
For body of mass \({m_2}\):
\({T_1} - {T_2} = {m_2}a\)
For body of mass \({m_3}\):
\({T_2} = {m_3}a\)
From the above three equation we get,
\(a = \frac{F}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}\)
And the tension between masses \({m_1}\) and \({m_2}\) is \({T_1} = \frac{{\left( {{m_2} + {m_3}} \right)}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\) and the tension between masses \({m_2}\) and \({m_3}\) is \({T_2} = \frac{{{m_3}}}{{\left( {{m_1} + {m_2} + {m_3}} \right)}}F\)

Motion of a Massive String:

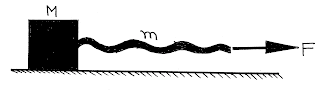
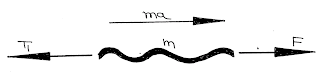
(1) A rope attached to a block at one end and a force applied to other end. Find the force applied by the rope on the block:

Body Attached to Massive String

FBD of Block

FBD of Rope

From free body diagram we get, 
For mass \(M\):
\({T_1} = Ma\)
For mass \(m\):
\(F - {T_1} = ma\)
From the above two equation we get Acceleration \(a = \frac{F}{{\left( {M + m} \right)}}\) and force or tension exerted on the block \({T_1} = Ma = \frac{M}{{\left( {M + m} \right)}}F\)

(2) A rope of mass \(m\) is attached to a block of mass \(M\) fixed t one end and a force applied to other end. Find the tension at the midpoint of the rope:

Body attached to Massive String

FBD of Half Rope

FBD of Half Rope

FBD of Block

From free body diagram we get, 
For mass \(M\):
\({T_1} = Ma\)
For half rope of mass \(\frac{m}{2}\):
\({T_2} - {T_1} = \frac{m}{2}a\)
or, \({T_2} - Ma = \frac{m}{2}a\)
or, \({T_2} = \left( {M + \frac{m}{2}} \right)a\)
For rest half of mass \(\frac{m}{2}\):
\(F - {T_2} = \frac{m}{2}a\)
or, \(F - \left( {M + \frac{m}{2}} \right)a = \frac{m}{2}a\)
or, \(F = \left( {M + m} \right)a\)
or, \(a = \frac{F}{{\left( {M + m} \right)}}\)
The force or tension exerted n the middle point of the rope is \({T_2} = \left( {M + \frac{m}{2}} \right)a = \left( {M + \frac{m}{2}} \right)\left( {\frac{F}{{M + m}}} \right) = \frac{{\left( {2M + m} \right)}}{{2\left( {M + m} \right)}}F\)

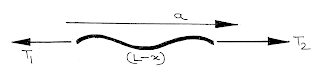
(3) A rope of mass \(m\) is attached to a block of mass \(M\) at one end and a force \(F\) is applied to other end of the rope. Find the tension to a distance \(x\) from the endpoint of the rope:

Body Attached to Massive String

FBD of Body

FBD of Rope of Length (L-x)

FBD of Rope of Length x

Suppose the length of the rope is \(L\), So mass per unit length is \(\frac{M}{L}\). 
From free body diagram we get,
For Mass \(M\):
\({T_1} = Ma\)
For the rope of length \(\left( {L - x} \right)\):
\({T_2} - {T_1} = \frac{{\left( {L - x} \right)m}}{L}a\)
or, \({T_2} - Ma = \frac{{\left( {L - x} \right)m}}{L}a\)
or, \({T_2} = \left[ {M + \frac{{\left( {L - x} \right)m}}{L}} \right]a\)
For rope of length \(x\):
\(F - {T_2} = \frac{{xM}}{L}a\)
or, \(F - \left[ {M + \frac{{\left( {L - x} \right)m}}{L}} \right]a = \frac{{xm}}{L}a\)
or, \(F = \left[ {\frac{{xm}}{L} + M + \frac{{\left( {L - x} \right)m}}{L}} \right]a\)
or, \(F = \left( {M + m} \right)a\)
or, \(a = \frac{F}{{\left( {M + m} \right)}}\)
Tension of the rope at a distance \(x\) from the end point \({T_2} = \left[ {M + \frac{{\left( {L - x} \right)m}}{L}} \right]a\)
or, \({T_2} = \left[ {M + \frac{{\left( {L - x} \right)m}}{L}} \right]\frac{F}{{\left( {M + m} \right)}} = \frac{{\left( {ML + mL - xm} \right)}}{{\left( {ML + mL} \right)}}F\) 

(4) A rope of length L is attached to one fixed end and a force F is applied to other end of the rope. Find the tension at a distance \(x\) from the endpoint of the rope:

A Massive String Attached to a Fixed End

FBD of Rope of Length (L-x)

FBD of Rope of Length x

Suppose mass of the rope is \(m\). From the free body diagram we get
For rope of length \(\left( {L - x} \right)\):
\(T = \frac{{\left( {L - x} \right)m}}{L}a\)
For rope of length :
\(F - T = \frac{{xm}}{L}a\)
or, \(F - \frac{{\left( {L - x} \right)m}}{L}a = \frac{{xm}}{L}a\)
or, \(F = \left[ {\frac{{xm}}{L} + \frac{{\left( {L - x} \right)m}}{L}} \right]a\)
or, \(F = ma\)
or, \(a = \frac{F}{m}\)

And the tension of the rope at the distance \(x\) from the end point is \(T = \frac{{\left( {L - x} \right)m}}{L}a\)
or, \[T = \frac{{\left( {L - x} \right)m}}{L} \times \frac{F}{m} = \frac{{\left( {L - x} \right)}}{L}F = \left( {1 - \frac{x}{L}} \right)F\]

(5) A rope of string which subjected to two forces applied to two end points. Find the tension at a distance \[x\] from one end:

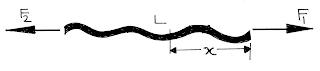A Rope Subjected to apply Force on Two End

FBD of Length (L-x)

FBD of Length x

From free body diagram we get,
For rope of length \(x\):
\({F_1} - T = \frac{{xm}}{L}a\)
For rope of length \(\left( {L - x} \right)\):
\(T - {F_2} = \frac{{\left( {L - x} \right)m}}{L}a\)
For entire rope of length \(L\):
\({F_1} - {F_2} = ma\)
or, \(a = \frac{{{F_1} - {F_2}}}{m}\)
And, \(T = {F_1} - \frac{{xm}}{L}a\)
or, \(T = {F_1} - \left( {\frac{{xm}}{L}} \right)\left( {\frac{{{F_1} - {F_2}}}{m}} \right)\)
or, \(T = {F_1} - \left( {\frac{x}{L}} \right)\left( {{F_1} - {F_2}} \right)\)
or, \(T = {F_1} - \frac{{x{F_1}}}{L} + \frac{{x{F_2}}}{L}\)
or, \(T = {F_1}\left( {1 - \frac{x}{L}} \right) + {F_2}\left( {\frac{x}{L}} \right)\)

(6) A rope vertically hanged and fixed at one end A force is applied to other end downward. Find the tension T at a distance \(x\) from the end point.

A Rope Hanged from a fixed End

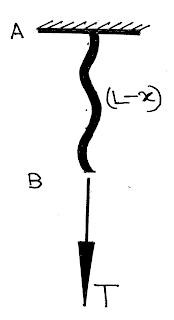FBD of Rope of Length (L-x)

FBD of Rope of Length x

    
From free body diagram we get,
For the rope of length \(\left( {L - x} \right)\):
\(T = \frac{{\left( {L - x} \right)m}}{L}a\)
For rope of length \(x\):
\(F - T = \frac{{xm}}{L}\)
For entire rope of length \(L\):
\(F = ma\)
or, \(a = \frac{F}{m}\)
And \(T = \frac{{\left( {L - x} \right)m}}{L}a\)
or, \(T = \frac{{\left( {L - x} \right)m}}{L} \times \left( {\frac{F}{m}} \right) = \left( {\frac{{L - x}}{L}} \right)F = \left( {1 - \frac{x}{L}} \right)F\)