NEET-JEE Essential Theory: Units and Measurement

Physical Quantities: All the quantities in terms of which laws of physics can be described and which can be measured are known a...

Units and Measurement

Tips And Tricks to Solve The Mechanics Problems Using Free Body Diagram: Part: II

Tips and Tricks to solve the Mechanics Problem using Free Body Diagram Part: 1

Physical Quantities:

All the quantities in terms of which laws of physics can be described and which can be measured are known as physical quantities.

Types of Physical Quantities:

There are two types of physical quantities:

(1) Fundamental quantities:

Those physical quantities which do not depends upon any other quantity are known as fundamental quantities or base quantities. There are seven fundamental or base quantities in SI system. They are Length, Mass, Time, Electric Current, Thermodynamic temperature, Amount of substance and Luminous intensity.

(2) Derived Quantities:

Those physical quantities which are derived from the fundamental quantities are known as derived quantities.

Example: $Speed = \frac{{Dis\tan ce}}{{Time}}$

Units:

The chosen reference standard of measurement in multiples of which, physical quantity is expressed is called the unit of that quantity.

System of Units:

The given table shows different system of units:

Type of Physical Quantities	Physical Quantities	System
		CGS (Originated in France)	MKS (Originated in France)	FPS (Originated in Britain)
Fundamental
	Length	cm	m	m
	Mass	g	kg	lb
	Time	s	s	s
Derived	Force	dyne	newton (N)	poundal
	Work	erg	joule (J)	ft-poundal
	Power	erg/s	watt (W)	ft-poundal/s

International System (S.I) of units:

This system is modification over the MKS system and so it is also known as Rationalised MKS system. Beside the three base units of MKS system, four fundamental and two supplementary units are also included in this system.

Classification of Units:

(1) Fundamental or base units:

Units of fundamental quantities are shown in below.

Base Quantities	SI Units
	Name	Symbol
Length	metre	m
Mass	kilogram	kg
Time	second	s
Electric Current	ampere	A
Thermodynamic temperature	kelvin	K
Amount of substance	mole	mol
Luminous intensity	candela	cd
Supplementary Units
Plane angle	radian	rad
Solid Angle	steradian	sr

(2) Derived units:
Units of derived quantities or the unit that can be expressed in terms of the base units.

(3) Supplementary units:
radian (rad) for plane angle and steradian (sr) for solid angle.

(4) Practical units:
Units defined for practical purposes. 
Example, light year (ly) is a practical unit of distance.

Representation of Errors:
Let a physical quantity $a$ be measured $n$ times. Let the measured values be ${a_1}$, ${a_2}$, ${a_3}$ ... ${a_n}$. To eliminate random error, their arithmetic mean is takenas the true value.
$\overline a  = \frac{{{a_1} + {a_2} + {a_3} + ... + {a_n}}}{n} = \frac{1}{n}\sum\limits_{i = 1}^n {{a_i}}$

Absolute error:
The magnitude of the difference between the true value and the measured value is called absolute error. Such errors are given by
$\Delta {a_1} = \overline a  - {a_1}$
$\Delta {a_2} = \overline a  - {a_2}$
$\Delta {a_3} = \overline a  - {a_3}$
... ... ... ... ...
$\Delta {a_n} = \overline a  - {a_n}$

Mean absolute error:

The arithmetic mean of the positive magnitudes of all the absolute errors is called mean absolute error.

$\Delta \overline a  = \frac{{\left| {\Delta {a_1}} \right| + \left| {\Delta {a_2}} \right| + \left| {\Delta {a_3}} \right| + ... + \left| {\Delta {a_n}} \right|}}{n} = \frac{1}{n}\sum\limits_{i = 1}^n {\left| {\Delta {a_i}} \right|}$

Relative error:

It is the ratio of the mean absolute error to the mean value.

Percentage error:

The relative error expressed in percent is called the percentage error.

Percentage error $= \frac{{\Delta \overline a }}{a} \times 100\%$

Propagation of errors in mathematical operations are listed in below chart:

Operation	Formula Z	Absolute error ∆Z	Relative error ∆Z/Z	Percentage error ∆Z/Z×100%
Sum	$A + B$	$\Delta A + \Delta B$	$\left( {\frac{{\Delta A + \Delta B}}{{A + B}}} \right)$	$\left( {\frac{{\Delta A + \Delta B}}{{A + B}}} \right) \times 100\%$
Difference	$A - B$	$\Delta A + \Delta B$	$\left( {\frac{{\Delta A + \Delta B}}{{A - B}}} \right)$	$\left( {\frac{{\Delta A + \Delta B}}{{A - B}}} \right) \times 100\%$
Multiplication	$A \times B$	$A\Delta B + B\Delta A$	$\left( {\frac{{\Delta A}}{A} + \frac{{\Delta B}}{B}} \right)$	$\left( {\frac{{\Delta A}}{A} + \frac{{\Delta B}}{B}} \right) \times 100\%$
Division	$\frac{A}{B}$	$\frac{{A\Delta B + B\Delta A}}{{{B^2}}}$	$\left( {\frac{{\Delta A}}{A} + \frac{{\Delta B}}{B}} \right)$	$\left( {\frac{{\Delta A}}{A} + \frac{{\Delta B}}{B}} \right) \times 100\%$
Power	${A^n}$	$n{A^{n - 1}}\Delta A$	$n\frac{{\Delta A}}{A}$	$n\frac{{\Delta A}}{A} \times 100\%$
Root	${A^{\frac{1}{n}}}$	$\frac{1}{n}{A^{\frac{1}{n} - 1}}\Delta A$	$\frac{1}{n}\frac{{\Delta A}}{A}$	$\frac{1}{n}\frac{{\Delta A}}{A} \times 100\%$

Dimensional Analysis:

Dimension of a physical quantity are the power or exponents to which the base quantities are raised to represent that quantity.

Derivation of Dimensional Formula:

The dimensional formulae of various physical quantities can be obtained by defining them in terms of simple quantities whose dimensions we already know

Example: $Volume = Length \times Breadth \times Height$

or, $Volume = \left[ L \right] \times \left[ L \right] \times \left[ L \right]$ $= \left[ {{L^3}} \right]$

Applications of Dimensional Analysis:

(1) To check the dimensional consistency of equations:

It is based on principle of homogeneity of dimensions which states that the equation is dimensionally correct if the dimensions of the various terms on either side of the equation are the same.

(2) To Deduce relation among the physical quantities:

If we know the dependence of the physical quantity on the other physical quantities, we can derive a relation among the physical quantities by using the principle of homogeneity of dimensions.

For example, let viscosity ($\eta$) of a gas depends upon the mass ($m$), the effective diameter ($d$) and the mean speed ($v$) of the molecules. We have to find $\eta$ as a function of these given variables.

Then, $\eta  \propto {m^a}{d^b}{v^c}$
or, $\eta  = k{m^a}{d^b}{v^c}$
Where, k, a, b, c are dimensionless constants.
Writing the dimensional formulae of the quantities on both sides of this equation.
$\left[ {M{L^{ - 1}}{T^{ - 1}}} \right] = {\left[ M \right]^a}{\left[ L \right]^b}{\left[ {L{T^{ - 1}}} \right]^c} = \left[ {{M^a}{L^{b + c}}{T^{ - c}}} \right]$
Comparing the dimensions on both sides we get, $a = 1$, $b + c =  - 1$, $- c =  - 1$
Then, $a = 1$, $c = 1$ and $b =  - 2$
Therefore, $\eta  = k{m^1}{d^{ - 2}}{v^1} = k\frac{{mv}}{{{d^2}}}$

(3) To convert one system of units into another system of units.
For this, we use the relation,
${n_2} = {n_1}{\left( {\frac{{{M_1}}}{{{M_2}}}} \right)^a}{\left( {\frac{{{L_1}}}{{{L_2}}}} \right)^b}{\left( {\frac{{{T_1}}}{{{T_2}}}} \right)^c}$
Where, ${M_1}$, ${L_1}$, ${T_1}$ are fundamental units on one system and ${M_2}$, ${L_2}$ and ${T_2}$ are fundamental units on the other system, a, b, c are the dimensions of the quantity in mass, length and time, ${n_1}$ is numerically value in one system and ${n_2}$ is its numerical value in the other system.

Note: This formula is valid only for absolute units and not for gravitational units.

Significant Figure:
The number of digits in the measured value which include certain digit plus one uncertain (doubtful) digit are called significant figures.

Rules for Counting the Significant Figures:
(1) Rule I: All non zero digit are significant.
(2) Rule II: All zeros occurring between the non-zero digits are significant, i.e.230089 contains six significant figures.
(3) Rule III: All zeros to the left of non-zero digit in a number with or without decimal point are not significant, i.e. 0.0023 contains two significant figures.
(4) Rule IV: All zeros to the right of non-zero digits in a number without decimal point are not significant, i.e. 23000 contains two significant figures.
(5) Rule V: The zeros to the right of non-zero digits (trailing zero) in a number with a decimal point are significant, i.e. 0.2300 contains four significant figures.

Remember:

Forget zeros on left but do not forget zeros on the right. Also please note that in scientific notation 23000 should be written as $23.000 \times {10^3}$. Thus 23 thousands is written as $23 \times {10^3}$ and it contains two significant figures. Similarly, 230 hundreds is written as $230 \times {10^2}$ and it contains three significant digits. Thus power (or exponent) of 10 is irrelevant in finding the significant figure in scientific notation. However, all the trailing zeros appearing in the base number in it are significant. The change of units only changes the order of exponent but not the number of significant figures. example: $1.40m = 1.40 \times {10^2}cm$, both have three significant figures.

Rules for Rounding off:

(1) Rule I: If the digit to be dropped is less than 5, then the preceding digit is left unchanged.

Example: 8.22 is rounded off to 8.2

(2) Rule II: If the digit to be dropped is more than 5, then the preceding digit is raised by one.

Example: 6.87 is rounded off to 6.9

(3) Rule III: If the digit to be dropped is 5 followed by digit other than zero, then the preceding digit is raised by one.

Example: 7.851 is rounded off to 7.9

(4) Rule IV: If the digit to be dropped is 5 or 5 followed by zero, then preceding digit is left unchanged, if it is even.

Example: 5.250 is rounded off 5.2

(5) Rule V: If the digit to be dropped is 5 or 5 followed by zero, then the preceding digit is raised by one, if it is odd.

Example: 3.750 is rounded off to 3.8

In addition or subtraction, the final result should retain as many decimal places as are there in the number with the least decimal places.

Example: $1.2 + 1.74 + 1.348 = 4.288$ 

The final result should be rounded off to 4.3

In multiplication or division, the final result should retain as many significant figures as are there in the original number with the least significant figures.
Example: $1.2 \times 1.74 \times 1.348 = 2.814624$
The final result should be 2.8

Measuring Instruments:

Vernier Callipers:
It is a device used to measure accurately upto ${\left( {\frac{1}{{10}}} \right)^{th}}$ of a millimeter. The vernier callipers is as shown in the figure.

Vernier constant:

It is the difference between values of one main scale division and one vernier scale division of vernier callipers. Let $n$ vernier scale division (VSD) coincide with $\left( {n - 1} \right)$ main scale division (MSD).

Therefore,   

$n$ VSD = $\left( {n - 1} \right)$ MSD
or, $1$ VSD$= \left( {\frac{{n - 1}}{n}} \right)MSD$
Vernier Constant, $VC = 1MSD - 1VSD$
or, $VC = 1MSD - \left( {\frac{{n - 1}}{n}} \right)MSD = \frac{1}{n}MSD$
or, $VC = \frac{{Value\_of\_one\_main\_scale\_division}}{{Total\_number\_of\_division\_on\_Vernier\_Scale}}$

Reading of Vernier callipers:
Place the body between the jaws and the zero of vernier scale lies ahead of  ${N^{th}}$ division of main scale. Then Main scale reading $\left( {MSR} \right) = N$
If ${n^{th}}$ division of vernier scale coincides with any division of main scale, then
Vernier scale reading $VSR = n \times VC$
Total Reading = $MSR + VSR = N + \left( {n \times VC} \right)$

Zero Error:

When the jaws A and B touch each other and if the zero of the vernier scale does not coincide with the zero of the main scale, then, the instrument has error called zero error. Zero error is always algebraically subtracted from the observed reading.

Positive zero error:

Zero error is said to be positive if the zero of the vernier scale lies on the right of the zero of the main scale as shown in figure

  
Here, zero error $= 0.00cm + (10 - 3) \times VC$

Negative Zero Error:

Zero error is said to be negative if the zero of the vernier scale lies on the left of the main scale as show in figure.

 Here, zero error $= 0.00 - (10 - 8) \times VC$  

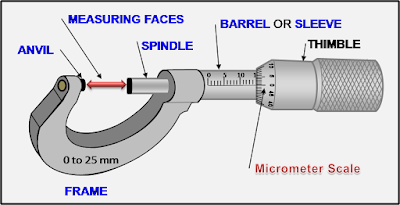
Screw Gauge:

It works on the principle of micrometer screw. A screw gauge is as shown in figure.

Pitch:

It is defined as the linear distance moved by the screw forward or backward when one complete rotation is given to the circular cap. Pitch of the screw $= \frac{{Dis\tan ce\_moved\_on\_linear\_scale}}{{Number\_of\_rotation}}$

Least count of the screw gauge $= \frac{{Pitch - of - the - screw}}{{Total - number - of - division - on - the - circular - scale}}$

Reading of a Screw gauge:
Place a wire between A and B, the edge of the cap lies ahead of ${N^{th}}$ division of linear scale. Then Linear scale reading (LSR) $= N$
If  ${n^{th}}$ division of circular scale lies over reference line, then
Circular scale reading (CSR) $= n \times (LC)$
Total Reading = LSR+CSR$= N + (n \times LC)$

Zero error:
When the two studs A and B of the screw gauge are brought in contact and if the zero of the circular scale does not coincide with the reference line then the screw gauge has an error. This error is called zero error.

Positive zero error:
Zero error is said to be positive if the zero of the circular scale lies below the reference line.
Here, zero error$=  + \left( {2 \times LC} \right)$

Negative zero error:
Zero error is said to be negative if the zero of the circular scale lies above the reference line.
Here, zero error$=  - \left( {2 \times LC} \right)$