Syllabus: (1) Reflection of light at spherical surface. (2)Geometry of Spherical Mirror. (3) Reflection in Spherical Mirror. ...
Syllabus:
(1) Reflection of light at spherical surface.
(2)Geometry of Spherical Mirror.
(3) Reflection in Spherical Mirror.
Example from daily life: Seeing the reflection of face in a spoon, steel bowl etc. Idea of a spherical surface (convex and concave). It should be mentioned that spoon, bowl etc. are only approximately spherical surfaces.
প্রাত্যহিক জীবন থেকে উদাহরণ: চামচ, স্টিলের বাটি ইত্যাদিতে দর্শকের মুখের প্রতিফলন পর্যবেক্ষণ এবং এর থেকে গোলীয় তলের ধারণা, উত্তল এবং অবতল।
Some definition: Center of curvature, radius of curvature, pole and principle axis of spherical mirror.
কয়েকটি সংজ্ঞা: বক্রতা কেন্দ্র, বক্রতা ব্যাসার্ধ্য, মেরু, প্রধান অক্ষ।
The knowledge of laws of reflection learned in class VII and VIII should be used for drawing ray diagrams in case of spherical mirrors. (Important: how to draw the normal for a spherical surface). Drawing of incident ray and reflected ray for a spherical mirror, many incident rays (Parallel, convergent and divergent) reflecting from the spherical mirror, and the concept of focus and focal length.
গোলীয় দর্পণে আপতিত ও প্রতিফলিত রশ্মিচিত্র অঙ্কন, সমান্তরাল, অপসারী এবং অভিসারী রশ্মিগুচ্ছের গোলীয় দর্পণে প্রতিফলন। ফোকাস ও ফোকাস দূরত্বের ধারণা।
Mechanism of image formation by ray diagram. The path of ray parallel to the principal axis after reflection, and the path of ray passing through the centre of curvature after reflection. Idea of paraxial rays and to show \(r = 2f\) for paraxial rays. Locating the image (both point object and extended object) by drawing ray diagrams (i) for concave mirror forming virtual magnified image (ii) for concave mirror forming real magnified image.
উপাক্ষীয় রশ্মির ধারণা ও উপাক্ষীয় রশ্মির ক্ষেত্রে \(r = 2f\) প্রমান
রেখাচিত্রের সাহায্যে বিন্দু বস্তু ও বিস্তৃত বস্তুর প্রতিবিম্ব গঠন ও বর্ণনা:
(i) অবতল দর্পণ দ্বারা অসদ্ ও বিবর্ধিত প্রতিবিম্ব গঠন।
(ii) অবতল দর্পণ দ্বারা সদ্ ও বিবর্ধিত প্রতিবিম্ব গঠন।
Dentist's mirror, rear view mirror of car and scooters etc. should be cited as examples. It should be mentioned that the rear view of mirror is used to create the parallel rays of light. By this process the driver of a car can see the far distant objects.
প্রয়োগ: দন্ত চিকিৎসকের ব্যবহৃত দর্পণ, গাড়ী, স্কুটারের ব্যবহৃত দর্পণ।
===================================
গোলীয় দর্পণ (Spherical Mirror): কোনও বক্র প্রতিফলক তল যদি কোনও গোলকের অংশবিশেষ হয়, তাহলে তাকে গোলীয় দর্পণ (Spherical Mirror) বলে।
এই গোলীয় দর্পণ দুই ধরণের হতে পারে।
(1) উত্তল দর্পণ (Convex Mirror)
(2) অবতল দর্পণ (Concave Mirror)
 |
| অবতল দর্পণ (Concave Mirror) |
 |
| উত্তল দর্পণ (Convex Mirror) |
অবতল দর্পণ (Concave Mirror): কোনও গোলীয় দর্পণের ভিতরের তল, প্রতিফলক তল হিসাবে কাজ করলে দর্পণটিকে অবতল দর্পণ (Concave Mirror) বলা হয়।
বা,
যে সকল গোলীয় দর্পণের বক্রতাকেন্দ্র, প্রতিফলক তলের সামনে থাকে, তাকে অবতল দর্পণ (Concave Mirror) বলে।
উত্তল দর্পণ (Convex Mirror): কোনও গোলীয় দর্পণের বাইরের তল, প্রতিফলক তল হিসাবে কাজ করলে দর্পণটিকে উত্তল দর্পণ (Convex Mirror) বলা হয়।
বা,
যে সকল গোলীয় দর্পণের বক্রতাকেন্দ্র, প্রতিফলক তলের পিছনে থাকে, তাকে উত্তল দর্পণ (Convex Mirror) বলে।
এখানে প্রতিফলক তল বক্র হলেও প্রতিফলনের সব সূত্রগুলিই প্রযোজ্য হয়। কিন্তু এক্ষেত্রে প্রতিবিম্বের আকার, অবস্থান ও প্রকৃতি সমতল দর্পণের মতো হয় না।
গোলীয় দর্পণে প্রতিফলনের সূত্র (Laws of Reflection at curved surface):
(1) আপতিত রশ্মি, প্রতিফলিত রশ্মি এবং আপতন বিন্দুতে প্রতিফলকের উপর অঙ্কিত অভিলম্ব একই সমতলে অবস্থান করে।
(2) আপতন কোন (\(\angle i\)) সর্বদা প্রতিফলন কোণের (\(\angle r\)) সমান হয়।
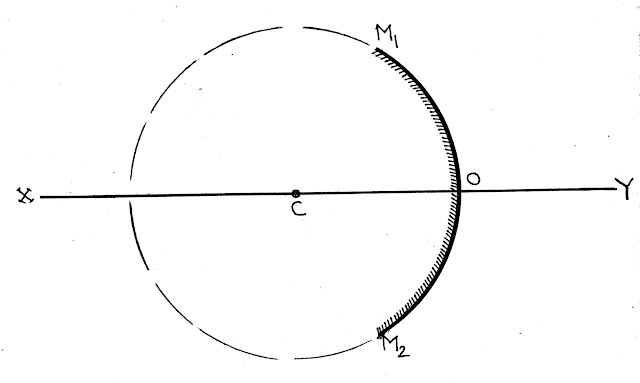
(1) মেরু (Pole): গোলীয় দর্পণের প্রতিফলক তলের মধ্যবিন্দুকে দর্পণের মেরু (Pole) বলা হয়।
নীচের চিত্রে O হল দর্পণের মেরু
(2) বক্রতা কেন্দ্র (Centre of curvature): কোনও গোলীয় দর্পণ যে গোলকের অংশবিশেষ, সেই গোলকের কেন্দ্রবিন্দুকে ওই দর্পণের বক্রতাকেন্দ্র (Centre of curvature) বলে।
নীচের চিত্রে \({M_1}O{M_2}\) দর্পণের \(C\) হল বক্রতা কেন্দ্র।
(3) বক্রতা ব্যাসার্ধ্য (Radius of curvature): কোনও গোলীয় দর্পণ যে গোলকের অংশবিশেষ, সেই গোলকের ব্যসার্ধ্যকে ওই দর্পণটির বক্রতা ব্যাসার্ধ্য (Radius of curvature) বলে। অর্থাৎ গোলীয় দর্পণের বক্রতা কেন্দ্র (Centre of curvature) থেকে মেরু (Pole) পর্যন্ত দৈর্ঘ্যকে বক্রতা ব্যাসার্ধ্য (Radius of curvature) বলে।
নীচের চিত্রে \({M_1}O{M_2}\) দর্পণের \(OC\) হল বক্রতা ব্যাসার্ধ্য।
(4) প্রধান অক্ষ (Principle Axis): গোলীয় দর্পণের মেরু (Pole) ও বক্রতা কেন্দ্রের সংযোগকারী সরলরেখাকে প্রধান অক্ষ বলে।
নীচের চিত্রে \({M_1}O{M_2}\) দর্পণের \(XY\) হল প্রধান অক্ষ।
(5) প্রধান ছেদ (Principle Section): কোনও গোলীয় দর্পণের প্রধান অক্ষের মধ্য দিয়ে আঁকা কোনও সমতল দর্পণটিকে যে বৃত্তচাপে ছেদ করে তাকে ওই দর্পণের প্রধান ছেদ (Principle Section) বলা হয়।
নীচের চিত্রে \({M_1}O{M_2}\) হল দর্পণের প্রধান ছেদ।
(6) উন্মেষ (Aperture): কোনও গোলীয় দর্পণের প্রধান ছেদের দুই প্রান্তবিন্দু যোগ করলে যে সরলরেখা পাওয়া যায়, তাকে ওই দর্পণের উন্মেষ (Aperture) বলা হয়। ওই সরলরেখা দর্পণের বক্রতা কেন্দ্রে যে কোণ উৎপন্ন করে, তাকে ওই দর্পণের কৌণিক উন্মেষ (Angular aperture) বলা হয়।
নীচের চিত্রে, \({M_1}O{M_2}\) দর্পণের \({M_1}{M_2}\) হল উন্মেষ এবং \(\angle {M_1}C{M_2}\) হল কৌণিক উন্মেষ ()।
গোলীয় দর্পণের আলোচনায় সর্বদা ক্ষুদ্র উন্মেষ যুক্ত দর্পণ ব্যবহার করা উচিত। যদি দর্পণের বক্রতা কেন্দ্রতে উৎপন্ন কোণ \(10^\circ \) অপেক্ষা কম হয়, তবে ওই দর্পণকে ক্ষুদ্র উন্মেষযুক্ত দর্পণ বলে গন্য করা হয়।
 |
| অবতল দর্পণের উন্মেষ ও কৌণিক উন্মেষ |
 |
| উত্তল দর্পণের উন্মেষ ও কৌণিক উন্মেষ |
উপাক্ষীয় রশ্মি (Paraxial Ray): যে সকল রশ্মি গোলীয় দর্পণের প্রধান অক্ষের সঙ্গে খুব কম কোণ করে এবং দর্পণের মেরুর খুব নিকটবর্তী অঞ্চলে আপতিত হয়, তাদের উপাক্ষীয় রশ্মি (Paraxial Ray) বলা হয়।
প্রান্তিক রশ্মি (Marginal Ray): যে সকল রশ্মি গোলীয় দর্পণে প্রধান অক্ষের সঙ্গে বেশি কোণে এবং দর্পণের মেরু থেকে দূরে অর্থাৎ দর্পণের প্রান্তে আপতিত হয়, তাদের প্রান্তিক রশ্মি (Marginal Ray) বলা হয়।
নীচের চিত্রে উপাক্ষীয় রশ্মি (Paraxial Ray) ও প্রান্তিক রশ্মি (Marginal Ray) দেখানো হল।
 |
| উপাক্ষীয় রশ্মি ও প্রান্তিক রশ্মি |
গোলীয় দর্পণের অভিলম্ব (Normal): যেকোনও গোলীয় দর্পণে যখন কোনও আলোকরশ্মি দর্পণের প্রতিফলক তলের উপর আপতিত হয় তখন সেই আপতন বিন্দু এবং বক্রতা কেন্দ্রের সংযোজক সরলরেখা দর্পণের উপর সর্বদা লম্ব হয়। এই লম্বকে গোলীয় দর্পণের ক্ষেত্রে অভিলম্ব বলা হয়।
কোনো সমান্তরাল রশ্মিগুচ্ছ গোলীয় দর্পণের প্রধান অক্ষের সাথে সমান্তরাল ভাবে এসে দর্পণের প্রতিফলক তলে আপতিত হলে প্রতিফলনের পর প্রতিফলিত রশ্মিগুচ্ছ প্রধান অক্ষের উপর একটি নির্দিষ্ট বিন্দুতে মিলিত হয় (অবতল দর্পণে) বা প্রধান অক্ষের উপর একটি নির্দিষ্ট বিন্দু থেকে অপসৃত হচ্ছে (উত্তল দর্পণে) বলে মনে হয়। এই বিন্দুটিকে গোলীয় দর্পণের মুখ্য ফোকাস বলে।
যদি কোনো সমান্তরাল রশ্মিগুচ্ছ প্রধান অক্ষের সাথে সমান্তরালে না এসে দর্পণের প্রতিফলক তলে আপতিত হয়, তখন ওই নির্দিষ্ট বিন্দুটি দর্পণের ফোকাস তলের কোনও একটি বিন্দুতে মিলিত হয় বা ফোকাস তলের একটি নির্দিষ্ট বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয়।
 |
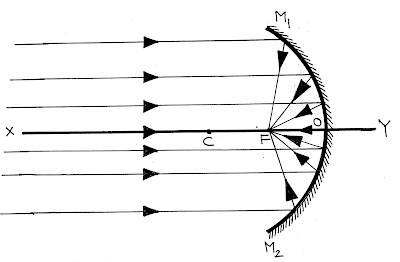| অবতল দর্পণের মুখ্য ফোকাস |
 |
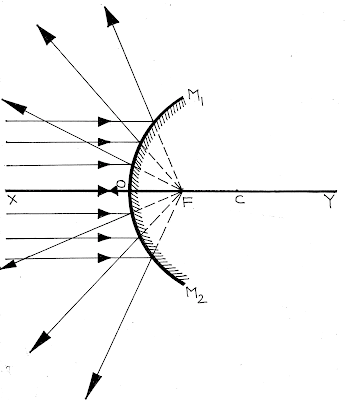| উত্তল দর্পণের মুখ্য ফোকাস |
 |
| অবতল দর্পণের ফোকাস তল |
 |
| উত্তল দর্পণের ফোকাস তল |
গোলীয় দর্পণের অপসারী রশ্মিগুচ্ছের প্রতিফলন:
আলোকরশ্মির প্রত্যাগমনের নীতি অনুযায়ী বলা যায় যে, যদি কোনো গোলীয় দর্পণের (অবতল দর্পণ) মুখ্য ফোকাস থেকে অপসারী আলোক রশ্মিগুচ্ছ নির্গত হয়ে দর্পণের প্রতিফলক তলে আপতিত হয়, তখন প্রতিফলনের পর ওই রশ্মিগুলি দর্পণ থেকে সমান্তরাল ভাবে নির্গত হয়।
 |
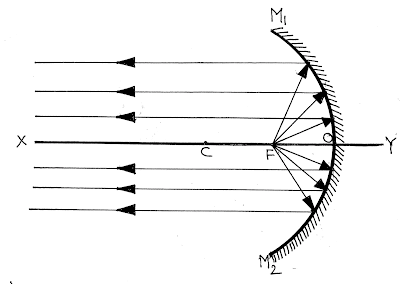| অবতল দর্পণের মুখ্য ফোকাস |
গোলীয় দর্পণে অভিসারী রশ্মিগুচ্ছের প্রতিফলন:
আলোকরশ্মির প্রত্যাগমনের নীতি অনুযায়ী বলা যায় যে, যদি কোনো গোলীয় দর্পণের (উত্তল দর্পণ) মুখ্য ফোকাসের দিকে অভিসারী রশ্মিগুচ্ছ ওই দর্পণের প্রতিফলক তলে আপতিত হয়, তখন প্রতিফলনের পর ওই রশ্মিগুলি দর্পণ থেকে সমান্তরালভাবে নির্গত হয়।
 |
| উ্তল দর্পণের মুখ্য ফোকাস |
মুখ্য ফোকাস (Principle focus ): কোনও সমান্তরাল রশ্মিগুচ্ছ কোনও গোলীয় দর্পণের প্রধান অক্ষের সঙ্গে সমান্তরাল ভাবে এসে দর্পণের উপর আপতিত হয়ে প্রতিফলনের পর প্রতিফলিত রশ্মিগুলি যদি প্রধান অক্ষের উপর একটি নির্দিষ্ট বিন্দুতে আপতিত হয় (অবতল দর্পণে) বা প্রধান অক্ষের উপর একটি নির্দিষ্ট বিন্দু থেকে অপসৃত হচ্ছে (উত্তল দর্পণে) বলে মনে হয়, তখন প্রধান অক্ষের উপর অবস্থিত ওই নির্দিষ্ট বিন্দুটিকে ওই গোলীয় দর্পণের মুখ্য ফোকাস (Principle Focus) বা ফোকাস বলে।
নীচের চিত্রে \(F\) হলো মুখ্য ফোকাস
ফোকাস দূরত্ব (Focal Length): গোলীয় দর্পণের মধ্যবিন্দু বা মেরু (Pole) থেকে মুখ্য ফোকাসের দূরত্বকে ফোকাস দূরত্ব (Focal Length) বলে।
নীচের চিত্রে \({M_1}O{M_2}\) দর্পণের \(OF\) হল ফোকাস দূরত্ব।
 |
| অবতল দর্পণের ফোকাস ও ফোকাস দূরত্ব |
 |
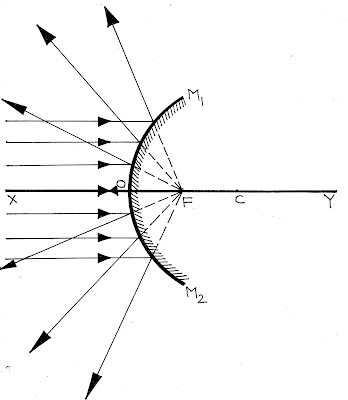| উত্তল দর্পণের ফোকাস ও ফোকাস দূরত্ব |
গোলীয় দর্পণে ফোকাস দূরত্ব (\(f\)) ও বক্রতা ব্যাসার্ধ্যের (\(r\)) মধ্যে সম্পর্ক:
কোনও গোলীয় দর্পণের ফোকাস দূরত্ব (\(f\)) সর্বদা তার বক্রতা ব্যাসার্ধ্যের (\(r\)) অর্ধেক হয়। কোনও গোলীয় দর্পণের বক্রতা ব্যাসার্ধ্য \(r\) এবং ফোকাস দূরত্ব \(f\) হলে,
\(f = \frac{r}{2}\)
বা, \(r = 2f\)
এখানে লক্ষণীয় যে, গোলীয় দর্পণের বক্রতা ব্যসার্ধ্য পারিপার্শ্বিক মাধ্যমের উপর নির্ভর করে না, তাই গোলীয় দর্পণের ফোকাস দৈর্ঘ্যও পারিপার্শ্বিক মাধ্যমের উপর নির্ভর করে না। অর্থাৎ দর্পণকে যে কোনও মাধ্যমেই রাখা হোক না কেন, ওর ফোকাস দৈর্ঘ্য সর্বদা অপরিবর্তিত থাকে।
অবতল দর্পণের ক্ষেত্রে প্রমাণ করো \(f = 2r\):
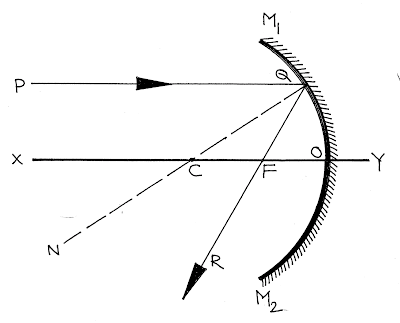
ধরাযাক \({M_1}O{M_2}\) অবতল দর্পণের \(C\), \(F\) এবং \(O\) হল অবতল দর্পণটির বক্রতা কেন্দ্র, ফোকাস এবং মেরু। তাই এখানে \(OC\) হল অবতল দর্পণটির বক্রতা ব্যাসার্ধ্য এবং \(OF\) হল ফোকাস দূরত্ব।
এখন প্রধান অক্ষের সাথে সমান্তরালভাবে একটি উপাক্ষীয় রশ্মি \(PQ\) দর্পণের \(Q\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর সেটি ফোকাসের মধ্য দিয়ে \(QR\) পথে প্রতিফলিত হয়। এখন \(QC\) যোগ করা হল। যেহেতু \(QC\) দর্পণের বক্রতা ব্যাসার্ধ্য তাই, \(QC\) রেখা \(Q\) বিন্দুতে দর্পণটির উপর লম্ব হবে।
এখন প্রতিফলনের সূত্রানুযায়ী লেখা যায়,
\(\angle PQC = \angle FQC\) [আপতন কোণ = প্রতিফলন কোণ]
আবার, \(\angle PQC = \angle FCQ\) [পরস্পর একান্তর কোণ]
সুতরাং, \(\angle FQC = \angle FCQ\)
তাই, \(FC = FQ\)
এখন উপাক্ষীয় রশ্মির ক্ষেত্রে \(Q\) এবং \(O\) বিন্দু কাছাকাছি থাকায় ধরা যায়, \(FC = FO\)
বা, \(FO = \frac{1}{2}OC\)
বা, \(f = \frac{r}{2}\)
বা, \(r = 2f\)
সুতরাং লেখা যায়, উপাক্ষীয় রশ্মির ক্ষেত্রে অবতল দর্পণের বক্রতা ব্যাসার্ধ্য, তার ফোকাস দূরত্বের দ্বিগুন হয়।
উত্তল দর্পণের ক্ষেত্রে প্রমান করো \(f = 2r\):
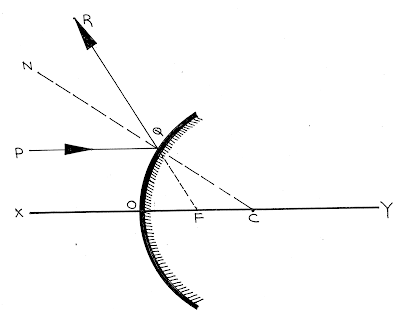
ধরাযাক \({M_1}O{M_2}\)উত্তল দর্পণের \(C\), \(F\) এবং \(O\) হল অবতল দর্পণের বক্রতা কেন্দ্র, ফোকাস বিন্দু এবং মেরু। তাই এখানে \(OC\) হল দর্পণের বক্রতা ব্যাসার্ধ্য এবং \(OF\) হল দর্পণের ফোকাস দূরত্ব।
এখন প্রধান অক্ষের সঙ্গে সমান্তরাল ভাবে একটি উপাক্ষীয় আলোকরশ্মি \(PQ\) দর্পণের \(Q\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর \(QR\) পথে প্রতিফলিত হয়। এখন \(CQ\) যোগ করে তাকে \(N\) পর্যন্ত বর্ধিত করা হল। যেহেতু \(QC\) দর্পণের বক্রতা ব্যাসার্ধ্য তাই, \(QN\) রেখা \(Q\) বিন্দুতে দর্পণের ওপর লম্ব হবে।
এখন প্রতিফলনের নিয়মানুযায়ী লেখা যায়,
\(\angle PQN = \angle RQN\) [আপতন কোণ = প্রতিফলন কোণ]
আবার, \(\angle PQN = \angle CQO\) [পরস্পর অনুরূপ কোণ]
আবার, \(\angle RQN = \angle FCQ\) [পরস্পর বিপ্রতীপ কোণ]
সুতরাং, \(\angle FCQ = \angle CQF\)
তাই, \(FC = FQ\)
এখন উপাক্ষীয় রশ্মির ক্ষেত্রে, \(Q\) এবং \(O\) বিন্দু কাছাকাছি থাকায় ধরা যায়, \(FC = FO\)
বা, \(FO = \frac{1}{2}OC\)
বা, \(f = \frac{r}{2}\)
বা, \(r = 2f\)
তাই লেখা যায়, উপাক্ষীয় রশ্মির ক্ষেত্রে উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য, তার ফোকাস দূরত্বের দ্বিগুন হয়।
গোলীয় দর্পণের (অবতল ও উত্তল) সমীকরণ:
কোনও গোলীয় দর্পণের মেরু থেকে বস্তু দূরত্ব \(u\) এবং প্রতিবিম্ব দূরত্ব \(v\) এবং দর্পণের ফোকাস দূরত্ব \(f\) হলে গোলীয় দর্পণের সমীকরণ হয়,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f} = \frac{2}{r}\)
Geometric or SI Sign Convention:
জ্যামিতিক আলোক বিজ্ঞানে দূরত্ব মাপার জন্য নানা ধরণের চিহ্নের রীতি ব্যবহার করা হয়ে থাকে তবে, এখানে আমরা সবথেকে সুবিধাজনক চিহ্নের রীতি হিসাবে কার্তেজীয় স্থানাঙ্কের চিহ্নের নীতি অনুসরণ করা হয়েছে। এই নীতি অনুযায়ী -
(1) গোলীয় দর্পণের মেরু থেকে সকল দূরত্ব মাপা হয়।
(2) আলোকরশ্মির আপতনের অভিমুখের দিকে মুলবিন্দু থেকে মাপা দূরত্বকে ধনাত্বক ও আলোকশ্মির আপতনের অভিমুখের বিপরীত দিকে মুলবিন্দু থেকে মাপা দূরত্বকে ঋনাত্বক ধরা হয়।
(3) প্রধান অক্ষের উপর লম্ব উপরের দিকের উচ্চতাকে ধনাত্বক ও নীচের দিকের উচ্চতাকে ঋনাত্বক ধরা হয়।
যেহেতু অবতল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব দর্পণের মেরু থেকে বাম দিকে অর্থাৎ আপতিত আলোকরশ্মির অভিমুখের বিপরীত দিকে মাপা হয়, তাই অবতল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব সর্বদা ঋনাত্বক ধরা হয়।
আবার যেহেতু উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দৈর্ঘ্য দর্পণের মেরু থেকে ডানদিকে অর্থাৎ আলোকরশ্মির অভিমুখেই মাপা হয়, তাই উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব সর্বদা ধনাত্বক হয়।
কোনও গোলীয় দর্পণের ফোকাস দূরত্ব (\(f\)) সর্বদা তার বক্রতা ব্যাসার্ধ্যের (\(r\)) অর্ধেক হয়। কোনও গোলীয় দর্পণের বক্রতা ব্যাসার্ধ্য \(r\) এবং ফোকাস দূরত্ব \(f\) হলে,
\(f = \frac{r}{2}\)
বা, \(r = 2f\)
এখানে লক্ষণীয় যে, গোলীয় দর্পণের বক্রতা ব্যসার্ধ্য পারিপার্শ্বিক মাধ্যমের উপর নির্ভর করে না, তাই গোলীয় দর্পণের ফোকাস দৈর্ঘ্যও পারিপার্শ্বিক মাধ্যমের উপর নির্ভর করে না। অর্থাৎ দর্পণকে যে কোনও মাধ্যমেই রাখা হোক না কেন, ওর ফোকাস দৈর্ঘ্য সর্বদা অপরিবর্তিত থাকে।
অবতল দর্পণের ক্ষেত্রে প্রমাণ করো \(f = 2r\):
এখন প্রধান অক্ষের সাথে সমান্তরালভাবে একটি উপাক্ষীয় রশ্মি \(PQ\) দর্পণের \(Q\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর সেটি ফোকাসের মধ্য দিয়ে \(QR\) পথে প্রতিফলিত হয়। এখন \(QC\) যোগ করা হল। যেহেতু \(QC\) দর্পণের বক্রতা ব্যাসার্ধ্য তাই, \(QC\) রেখা \(Q\) বিন্দুতে দর্পণটির উপর লম্ব হবে।
এখন প্রতিফলনের সূত্রানুযায়ী লেখা যায়,
\(\angle PQC = \angle FQC\) [আপতন কোণ = প্রতিফলন কোণ]
আবার, \(\angle PQC = \angle FCQ\) [পরস্পর একান্তর কোণ]
সুতরাং, \(\angle FQC = \angle FCQ\)
তাই, \(FC = FQ\)
এখন উপাক্ষীয় রশ্মির ক্ষেত্রে \(Q\) এবং \(O\) বিন্দু কাছাকাছি থাকায় ধরা যায়, \(FC = FO\)
বা, \(FO = \frac{1}{2}OC\)
বা, \(f = \frac{r}{2}\)
বা, \(r = 2f\)
সুতরাং লেখা যায়, উপাক্ষীয় রশ্মির ক্ষেত্রে অবতল দর্পণের বক্রতা ব্যাসার্ধ্য, তার ফোকাস দূরত্বের দ্বিগুন হয়।
এখন প্রধান অক্ষের সঙ্গে সমান্তরাল ভাবে একটি উপাক্ষীয় আলোকরশ্মি \(PQ\) দর্পণের \(Q\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর \(QR\) পথে প্রতিফলিত হয়। এখন \(CQ\) যোগ করে তাকে \(N\) পর্যন্ত বর্ধিত করা হল। যেহেতু \(QC\) দর্পণের বক্রতা ব্যাসার্ধ্য তাই, \(QN\) রেখা \(Q\) বিন্দুতে দর্পণের ওপর লম্ব হবে।
এখন প্রতিফলনের নিয়মানুযায়ী লেখা যায়,
\(\angle PQN = \angle RQN\) [আপতন কোণ = প্রতিফলন কোণ]
আবার, \(\angle PQN = \angle CQO\) [পরস্পর অনুরূপ কোণ]
আবার, \(\angle RQN = \angle FCQ\) [পরস্পর বিপ্রতীপ কোণ]
সুতরাং, \(\angle FCQ = \angle CQF\)
তাই, \(FC = FQ\)
এখন উপাক্ষীয় রশ্মির ক্ষেত্রে, \(Q\) এবং \(O\) বিন্দু কাছাকাছি থাকায় ধরা যায়, \(FC = FO\)
বা, \(FO = \frac{1}{2}OC\)
বা, \(f = \frac{r}{2}\)
বা, \(r = 2f\)
তাই লেখা যায়, উপাক্ষীয় রশ্মির ক্ষেত্রে উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য, তার ফোকাস দূরত্বের দ্বিগুন হয়।
গোলীয় দর্পণের (অবতল ও উত্তল) সমীকরণ:
কোনও গোলীয় দর্পণের মেরু থেকে বস্তু দূরত্ব \(u\) এবং প্রতিবিম্ব দূরত্ব \(v\) এবং দর্পণের ফোকাস দূরত্ব \(f\) হলে গোলীয় দর্পণের সমীকরণ হয়,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f} = \frac{2}{r}\)
Geometric or SI Sign Convention:
জ্যামিতিক আলোক বিজ্ঞানে দূরত্ব মাপার জন্য নানা ধরণের চিহ্নের রীতি ব্যবহার করা হয়ে থাকে তবে, এখানে আমরা সবথেকে সুবিধাজনক চিহ্নের রীতি হিসাবে কার্তেজীয় স্থানাঙ্কের চিহ্নের নীতি অনুসরণ করা হয়েছে। এই নীতি অনুযায়ী -
(1) গোলীয় দর্পণের মেরু থেকে সকল দূরত্ব মাপা হয়।
(2) আলোকরশ্মির আপতনের অভিমুখের দিকে মুলবিন্দু থেকে মাপা দূরত্বকে ধনাত্বক ও আলোকশ্মির আপতনের অভিমুখের বিপরীত দিকে মুলবিন্দু থেকে মাপা দূরত্বকে ঋনাত্বক ধরা হয়।
(3) প্রধান অক্ষের উপর লম্ব উপরের দিকের উচ্চতাকে ধনাত্বক ও নীচের দিকের উচ্চতাকে ঋনাত্বক ধরা হয়।
যেহেতু অবতল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব দর্পণের মেরু থেকে বাম দিকে অর্থাৎ আপতিত আলোকরশ্মির অভিমুখের বিপরীত দিকে মাপা হয়, তাই অবতল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব সর্বদা ঋনাত্বক ধরা হয়।
আবার যেহেতু উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দৈর্ঘ্য দর্পণের মেরু থেকে ডানদিকে অর্থাৎ আলোকরশ্মির অভিমুখেই মাপা হয়, তাই উত্তল দর্পণের বক্রতা ব্যাসার্ধ্য ও ফোকাস দূরত্ব সর্বদা ধনাত্বক হয়।
| Distance | Quantity | Symbol |
|---|---|---|
| From the pole to the object | Object-distance | u |
| From the pole to the image | Image-distance | v |
| From the pole to the focus | Focal length | f |
| From the pole to the center | Radius of curvature | r |
| Height of the object | Object-height | \({h_o}\) |
| Height of the image | Image-height | \({h_i}\) |
 |
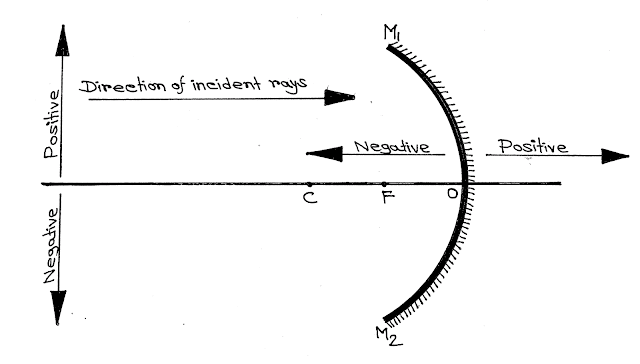| Sign Convention For Concave Mirror |
 |
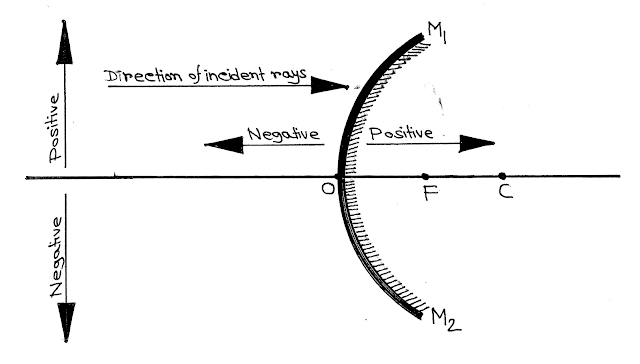| Sign Convention For Convex Mirror |
প্রতিবিম্বের আকার ও বস্তুর আকারের অনুপাতকে রৈখিক বিবর্ধন (Linear Magnification) বলে।
যদি প্রতিবিম্বের উচ্চতা \({h_i}\) এবং বস্তুর উচ্চতা \({h_o}\) হয়, তাহলে রৈখিক বিবর্ধন (Linear Magnification) \( = m = \frac{{{h_i}}}{{{h_o}}}\)
 |
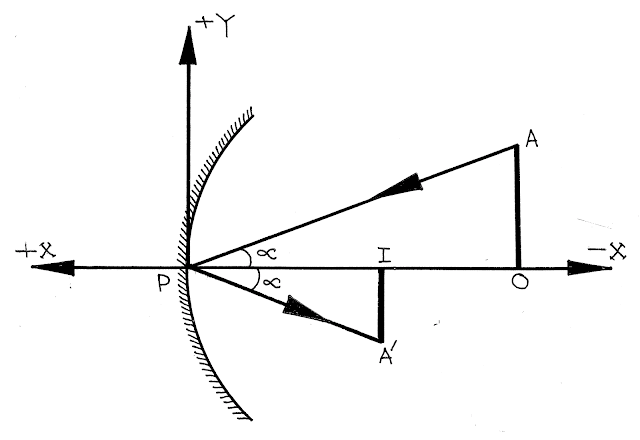| Linear Magnification |
বা, \(\frac{{{A^/}I}}{{AO}} = \frac{{PI}}{{PO}}\)
এখন কার্তেজীয় নির্দেশতন্ত্রেরনিয়মানুযায়ী চিহ্নের রীতি থেকে লেখা যায়,
\(u = - PO\)
\(v = - PI\)
\({h_o} = + AO\)
\({h_i} = - {A^/}I\)
সুতরাং \(\frac{{ - {h_i}}}{{{h_o}}} = \frac{{ - v}}{{ - u}}\)
বা, \(\frac{{{h_i}}}{{{h_o}}} = - \frac{v}{u}\)
সুতরাং রৈখিক বিবর্ধন \( = \frac{{{h_i}}}{{{h_o}}} = - \frac{v}{u}\)
এই রৈখিক বিবর্ধনের মান ধনাত্বক ও ঋনাত্বক হতে পারে। রৈখিক বিবর্ধন \(m\) এর মান ঋনাত্বক হলে প্রতিবিম্বটি বস্তু সাপেক্ষে অবশীর্ষ হবে এবং রৈখিক বিবর্ধনের মান ধনাত্বক হলে প্রতিবিম্বটি বস্তু সাপেক্ষে সমশীর্ষ হবে।
আমরা কোনও গানিতিক সমস্যা সমাধানের সময় প্রতিবিম্বের অবস্থান ও প্রকৃতি জানতে হলে ওই দর্পণের ফোকাস দূরত্ব, বস্তুর অবস্থান, প্রতিবিম্বের অবস্থান ইত্যাদি কার্তেজীয় স্থানাঙ্ক অনুযায়ী বসাতে হয়। এক্ষেত্রে দর্পণের উপর আপতিত আলোকরশ্মির অভিমুখকে ধনাত্বক \(X\) অক্ষ এবং দর্পণের মেরু থেকে উপরের দিককে ধনাত্বক \(Y\) অক্ষ ধরে নেওয়া হয়।
সদ্ (Real) বস্তুর ক্ষেত্রে, মেরু থেকে মাপা সকল বস্তু দূরত্বকে ঋনাত্বক ধরা হয় এবং অসদ্ বস্তুর ক্ষেত্রে মেরু থেকে মাপা বস্তু দূরত্ব সর্বদা ধনাত্বক ধরা হয়।
সদ্ বস্তুর ক্ষেত্রে যেহেতু মেরু থেকে মাপা বস্তু দূরত্ব ঋনাত্বক ধরা হয়, তাই প্রতিবিম্ব দূরত্ব ঋনাত্বক হলে বুঝতে হবে, বস্তুটি দর্পণের যেপাশে অবস্থিত, প্রতিবিম্বটিও দর্পণের সেইপাশে অবস্থিত হবে।
আবার প্রতিবিম্ব দূরত্ব ধনাত্বক হলে বুঝতে হবে, বস্তুটি দর্পণের যেপাশে অবস্থিত তার বিপরীত দিকে প্রতিবিম্বটি অবস্থিত হবে। প্রতিবিম্ব দূরত্ব ধনাত্বক বা ঋনাত্বক দেখে প্রতিবিম্বের প্রকৃতি সম্পর্কে কিছু তথ্য জানা যায় না। প্রতিবিম্ব দূরত্ব ধনাত্বক বা ঋনাত্বক হলে প্রতিবিম্বটির অবস্থান সম্পর্কে একটি স্বচ্ছ ধারণা পাওয়া যায়।
ফোকাস দূরত্ব (\(v\)) এর তাৎপর্য (Interpretation of \(v\) ):
সাধারনত গোলীয় দর্পন দুই ধরণের হয়। একটি উত্তল দর্পণ অন্যটি অবতল দর্পণ। কার্তেজীয় স্থানাঙ্ক রীতি অনুসারে অবতল দর্পণের ফোকাস দূরত্ব সর্বদা ঋনাত্বক এবং উত্তল দর্পণের ফোকাস দূরত্ব সর্বদা ধনাত্বক হয়।
রৈখিক বিবর্ধন (\(m\)) এর তাৎপর্য (Interpretation of \(m\)):
কোনও দর্পণের প্রতিবিম্বের রৈখিক বিবর্ধনের (\(m\)) চিহ্ন থেকে প্রতিবিম্বটির প্রকৃতি সম্পর্কে একটি স্বচ্ছ ধারণা পাওয়া যায়। এই রৈখিক বিবর্ধনের চিহ্ন থেকে প্রতিবিম্বটি সদ্ বা অসদ্ তা বোঝা যায়।
একটি বস্তু কোনও অবতল দর্পণের ডালপাশে রাখা হলে, প্রতিবিম্বটিও যদি ডানপাশে অবস্থিত হয়, তাহলে \(u = - ve\) এবং \(v = - ve\) এবং
\(m = - \frac{v}{u} = - \frac{{\left( { - v} \right)}}{{\left( { - u} \right)}} = - \frac{v}{u} = Negative - Value\)
যেহেতু \(m = \frac{{{h_i}}}{{{h_o}}}\) একটি ঋনাত্বক মান তাই এখানে \(m\) নির্দেশ করে প্রতিবিম্বটি অবশীর্ষ এবং সদ্। এখানে \(m\) ঋনাত্বক হওয়ায় বলা যায় সদ্ বস্তুর সদ্ প্রতিবিম্ব এবং অসদ্ বস্তুর অসদ্ প্রতিবিম্ব গঠন করবে। আবার অনুরূপভাবে \(m\) যদি ধনাত্বক হয় তখন বুঝতে হবে প্রতিবিম্বটি সমশীর্ষ এবং সদ্ বস্তুর অসদ্ প্রতিবিম্ব এবং অসদ্ বস্তুর সদ্ প্রতিবিম্ব গঠন করবে।
গোলীয় দর্পণের সামনে বস্তু রাখলে প্রতিবিম্ব গঠিত হয়। এই প্রতিবিম্বের অবস্থান ও প্রকৃতি নির্ণয় করার জন্য ওই দর্পণের ফোকাস ও বক্রতা কেন্দ্রের ধর্মকে কাজে লাগানো হয়।
(1) ফোকাস বিন্দুর মধ্য দিয়ে যাওয়া কোনও আলোকরশ্মি: ফোকাস বিন্দুর মধ্য দিয়ে যাওয়া কোনও আলোকরশ্মি গিয়ে দর্পণের উপর আপতিত হলে তা প্রধান অক্ষের সমান্তরাল ভাবে নির্গত হয়।
(2) প্রধান অক্ষের সমান্তরাল ভাবে যাওয়া কোনও আলোকরশ্মি: প্রধান অক্ষের সমান্তরাল ভাবে গিয়ে কোনও আলোকরশ্মি দর্পণের উপর আপতিত হলে তা সর্বদা ওই গোলীয় দর্পণের ফোকাস বিন্দুর মধ্য দিয়ে যাবে।
(3) বক্রতা কেন্দ্রের মধ্য দিয়ে যাওয়া কোনও আলোকরশ্মি: বক্রতাকেন্দ্র হল ওই গোলীয় দর্পণ যে গোলকের অংশবিশেষ তার কেন্দ্র। তাই বক্রতাকেন্দ্রের মধ্য দিয়ে গিয়ে দর্পণে আপতিত হওয়ার অর্থ হল দর্পণে লম্বভাবে আপতিত হওয়া। তাই এক্ষেত্রে রশ্মি যে পথে আপতিত হয়, প্রতিফলিত রশ্মি সেই পথেই ফিরে যাবে।
বস্তুকে মেরু ও ফোকাসের মাঝে রাখা হল:
ধরাযাক, \({M_1}O{M_2}\) একটি অবতল দর্পণের মেরু, ফোকাস ও বক্রতাকেন্দ্র যথাক্রমে \(O\), \(F\) এবং \(C\)। এবং এই দর্পণের \(XY\) হল প্রধান অক্ষ। এখন একটি বস্তু \(PQ\) কে প্রধান অক্ষের উপর মেরু (\(O\)) এবং ফোকাসের (\(F\)) মাঝে রাখা হল। এখন \(P\) বিন্দু থেকে নির্গত দুটি আলোকরশ্মির একটি \(PA\) দর্পণের প্রধান অক্ষের সমান্তরালভাবে \(A\) বিন্দুতে আপতিত হয়ে \(AS\) পথে ফোকাস দিয়ে বেরিয়ে যায়। এবং অপর একটি আলোকরশ্মি \(PB\) দর্পণের উপর লম্বভাবে \(B\) বিন্দুতে আপতিত হয়ে \(BR\) পথেই নির্গত হয়। এখন এই দুটি রশ্মি \(AS\) এবং \(BR\) কে পিছনের দিকে বর্ধিত করলে তারা যথাক্রমে \({P^/}\) বিন্দুতে মিলিত হয়। এই \({P^/}\) বিন্দু থেকে প্রধান অক্ষের উপর একটি লম্ব কল্পনা করা হল। এই \({P^/}{Q^/}\) হল এখানে \(PQ\) বস্তুর অসদ্ প্রতিবিম্ব।
এখানে,
বস্তুর অবস্থান: দর্পণের মেরু ও ফোকাসের মাঝে।
প্রতিবিম্বের অবস্থান: দর্পণের যেপাশে বস্তু অবস্থিত তার বিপরীত পাশে অর্থাৎ দর্পণের পিছনে
প্রতিবিম্বের প্রকৃতি:
(1) প্রতিবিম্বটি অসদ্
(2) প্রতিবিম্বটি সমশীর্ষ
(3) প্রতিবিম্বটি বস্তু অপেক্ষা বড়ো অর্থাৎ বিবর্ধিত
গানিতিক ব্যাখ্যা:
ধরাযাক,
\(u = - x\)
\(f = - z\)
এখন দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{x} + \frac{1}{v} = - \frac{1}{z}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\)
এক্ষেত্রে, \(x < z\), তাই \(\frac{1}{x} > \frac{1}{z}\)
সুতরাং \(\frac{1}{v}\) একটি ধনাত্বক রাশি এবং \(v\) একটি ধনাত্বক রাশি।
সুতরাং প্রতিবিম্বটি দর্পণের পিছনে অবস্থিত হবে।এখন রৈখিক বিবর্ধন \(m = - \frac{v}{u} = - \frac{v}{{ - x}} = + \frac{v}{x} > 1\)
এখানে \(\left( {\frac{1}{v} - \frac{1}{x}} \right)\) একটি ঋনাত্বক রাশি, তাই
\(\frac{1}{x} > \frac{1}{v}\)
বা, \(\frac{1}{x} < \frac{1}{v}\)
সুতরাং \(m = - \frac{v}{u} = - \frac{v}{{ - x}} = + \frac{v}{x} > 1\)
সুতরাং এখানে \(m\) ধনাত্বক, তাই
(i) সদ্ বস্তুর অসদ্ প্রতিবিম্ব গঠিত হয়।
(ii) প্রতিবিম্বটি সমশীর্ষ হবে।
(iii) \(m > 1\), তাই প্রতিবিম্বটি বিবর্ধিত হবে।
বস্তুটিকে ফোকাসে রাখা হল:
ধরাযাক,
\(u = - x\)
\(f = - z\)
এখন দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{x} + \frac{1}{v} = - \frac{1}{z}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\)
এক্ষেত্রে, \(x < z\), তাই \(\frac{1}{x} > \frac{1}{z}\)
সুতরাং \(\frac{1}{v}\) একটি ধনাত্বক রাশি এবং \(v\) একটি ধনাত্বক রাশি।
সুতরাং প্রতিবিম্বটি দর্পণের পিছনে অবস্থিত হবে।এখন রৈখিক বিবর্ধন \(m = - \frac{v}{u} = - \frac{v}{{ - x}} = + \frac{v}{x} > 1\)
এখানে \(\left( {\frac{1}{v} - \frac{1}{x}} \right)\) একটি ঋনাত্বক রাশি, তাই
\(\frac{1}{x} > \frac{1}{v}\)
বা, \(\frac{1}{x} < \frac{1}{v}\)
সুতরাং \(m = - \frac{v}{u} = - \frac{v}{{ - x}} = + \frac{v}{x} > 1\)
সুতরাং এখানে \(m\) ধনাত্বক, তাই
(i) সদ্ বস্তুর অসদ্ প্রতিবিম্ব গঠিত হয়।
(ii) প্রতিবিম্বটি সমশীর্ষ হবে।
(iii) \(m > 1\), তাই প্রতিবিম্বটি বিবর্ধিত হবে।
বস্তুটিকে ফোকাসে রাখা হল:
ধরাযাক, \({M_1}O{M_2}\) দর্পণের \(O\), \(F\) এবং \(C\) হল যথাক্রমে দর্পণের মেরু, ফোকাস এবং বক্রতা কেন্দ্র। এবং এই দর্পণের \(XY\) হল প্রধান অক্ষ।
এখন দর্পণটির ফোকাস বিন্দুতে একটি বস্তু \(PQ\) রাখা হল। এই \(P\) বিন্দু থেকে নির্গত আলোকরশ্মি একটি রশ্মি \(PA\) দর্পণটির প্রধান অক্ষের সাথে সমান্তরালভাবে গিয়ে \(A\) বিন্দুতে আপতিত হয়। এবং প্রতিফলনের পর রশ্মিটি ফোকাস বিন্দু \(F\) দিয়ে \(AS\) পথে নির্গত হয়। এবং অপর একটি আলোকরশ্মি \(PB\) দর্পণের উপর লম্বভাবে \(B\) বিন্দুতে আপতিত হয়ে \(BR\) পথে নির্গত হয়। এই \(AS\) এবং \(BR\) রশ্মিদুটি অসীমে গিয়ে মিলিত হয়, তাই এক্ষেত্রে প্রতিবিম্বটি অসীম দূরত্বে এবং অবশীর্ষ ও অনেকগুন বিবর্ধিত প্রতিবিম্ব গঠন করে।
বস্তুর অবস্থান: ফোকাস বিন্দুতে
প্রতিবিম্বের অবস্থান: অসীমে
প্রতিবিম্বের প্রকৃতি:
(i) প্রতিবিম্বটি সদ্ হবে।
(ii) প্রতিবিম্বটি অসীমে অবস্থিত হবে।
(iii) প্রতিবিম্বটি অবশীর্ষ হবে।
গানিতিক ব্যাখ্যা:
এখানে ধরাযাক,
\(u = - f = - z\)
\(f = - z\)
এখন গোলীয় দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{z} + \frac{1}{v} = - \frac{1}{f}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{z} - \frac{1}{z}} \right) = 0\)
বা, \(v = \frac{1}{0}\)
বা, \(v = \frac{1}{0} = \infty \)
সুতরাং প্রতিবিম্বটি অসীমে গঠিত হবে।
আবার রৈখিক বিবর্ধন (\(m\)) \( = - \frac{v}{u} = - \frac{\infty }{{ - z}} = + \infty \)
সুতরাং প্রতিবিম্বটি অনেকগুন বিবর্ধিত হবে।
বস্তুকে ফোকাস ও বক্রতাকেন্দ্রের মধ্যে রাখা হল।
এখন দর্পণটির ফোকাস ও বক্রতা কেন্দ্রের মধ্যে একটি বস্তু \(PQ\) রাখা হল। এই \(P\) বিন্দু থেকে নির্গত একটি আলোকরশ্মি \(PA\) প্রধান অক্ষের সাথে সমান্তরাল ভাবে দর্পণের \(A\) বিন্দুতে আপতিত হয় এবং তা দর্পণের ফোকাস বিন্দু \(F\) এর মধ্য দিয়ে \(A{P^/}\) পথে নির্গত হয়। এবং অপর একটি আলোকরশ্মি \(PB\) দর্পণের উপর লম্বভাবে \(B\) বিন্দুতে আপতিত হয়ে \(B{P^/}\) পথে ফিরে আসে। এখানে এই রশ্মি দুটি \({P^/}\) বিন্দুতে মিলিত হয়। এখন \({P^/}\) বিন্দু থেকে দর্পণের প্রধান অক্ষের উপর \({P^/}{Q^/}\) লম্ব টানা হল। এখানে এই \({P^/}{Q^/}\) হল \(PQ\) বস্তুর সদ্ প্রতিবিম্ব।
বস্তুর অবস্থান: দর্পণের ফোকাস ও বক্রতাকেন্দ্রের মধ্যে।
প্রতিবিম্বের অবস্থান: বক্রতা কেন্দ্রের বাইরে
প্রতিবিম্বের প্রকৃতি:
(i) প্রতিবিম্বটি সদ্ হবে।
(ii) প্রতিবিম্বটি অবশীর্ষ হবে।
(iii) প্রতিবিম্বটি বিবর্ধিত হবে।
এখানে ধরাযাক,
\(u = - x\)
\(f = - z\)
এখন গোলীয় দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{x} + \frac{1}{v} = - \frac{1}{z}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\)
এখানে, \(x > z\) তাই \(\frac{1}{x} < \frac{1}{z}\)
তাই, \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\) একটি ঋনাত্বক রাশি। অর্থাৎ এখানে \(\frac{1}{v}\) একটি ঋনাত্বক রাশি
সুতরাং \(v\) ঋনাত্বক।
সুতরাং বস্তুটি দর্পণের যেপাশে অবস্থিত প্রতিবিম্বটিও সেই পাশে অবস্থিত হবে।
আবার \(m = - \frac{v}{u} = - \frac{{ - v}}{{ - x}} = - \frac{v}{x}\) এবং \(\left( {\frac{1}{v} - \frac{1}{x}} \right)\) তাই \(\frac{1}{x} > \frac{1}{v}\)
বা, \(v > x\)
সুতরাং \(\left| m \right| = \left| {\frac{v}{x}} \right| > 1\)
তাই যেহেতু \(m\) ঋনাত্বক এবং বস্তুটি সদ্, তাই প্রতিবিম্বটিও সদ্ হবে। আবার যেহেতু \(m\) ঋনাত্বক তাই প্রতিবিম্বটি অবশীর্ষ হবে আবার \(m\)>1 তাই প্রতিবিম্বটি বিবর্ধিত হবে।
বস্তুকে বক্রতাকেন্দ্রেই রাখা হল:
এখন দর্পণটির বক্রতা কেন্দ্রে একটি বস্তু \(PQ\) রাখা হল। এই \(Q\) বিন্দু থেকে নির্গত একটি আলোকরশ্মি \(QA\) প্রধান অক্ষের সাথে সমান্তরাল ভাবে দর্পণের \(A\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর তা ফোকাস দিয়ে \(A{Q^/}\) পথে নির্গত হয়। এবং অপর একটি আলোকরশ্মি \(QB\) দর্পণটির ফোকাসের মধ্য দিয়ে গিয়ে দর্পণের উপর লম্বভাবে \(B\) বিন্দুতে আপতিত হয়ে তা প্রধান অক্ষের সাথে সমান্তরাল ভাবে \(B{Q^/}\) পথে নির্গত হয়।
এখানে এই \(A{Q^/}\) এবং \(B{Q^/}\) রশ্মিদুটি যথাক্রমে বক্রতা কেন্দ্রেই \(Q\) বিন্দুতে মিলিত হয়। এই \(Q\) বিন্দু থেকে প্রধান অক্ষের উপর \({P^/}{Q^/}\) লম্ব টানা হল। এখানে এই \({P^/}{Q^/}\) হল \(PQ\) এর সদ্ প্রতিবিম্ব।
বস্তুর অবস্থান: বক্রতা কেন্দ্র
প্রতিবিম্বের অবস্থান: বক্রতা কেন্দ্রে
প্রতিবিম্বের প্রকৃতি:
(i) প্রতিবিম্বটি সদ্ হবে
(ii) প্রতিবিম্বটি অবশীর্ষ হবে
(iii) প্রতিবিম্বটি বস্তুর আকারের সমান হবে।
ধরাযাক,
\(u = - x\) এবং
\(x = \left| r \right| = \left| {2f} \right| = 2z\)
\(f = - z\)
গোলীয় দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{{2z}} + \frac{1}{v} = - \frac{1}{z}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{{2z}} - \frac{1}{z}} \right) = - \frac{1}{{2z}}\)
বা, \(v = - 2z = - 2f = - r\)
সুতরাং প্রতিবিম্বটি বক্রতাকেন্দ্রেই গঠিত হবে।
আবার \(m = - \frac{v}{u} = - \frac{{ - 2z}}{{ - 2z}} = - 1\)
এখানে \(m\) ঋনাত্বক, এবং বস্তুটি সদ্ তাই প্রতিবিম্বটিও সদ্ হবে। আবার \(m\) ঋনাত্বক হওয়ায় প্রতিবিম্বটিও অবশীর্ষ হবে। আবার, \(\left| m \right|\) =1, তাই প্রতিবিম্বটি বস্তুর আকারের সমান হবে।
বস্তুটি বক্রতা কেন্দ্রের বাইরে কিন্তু অসীমের মধ্যে অবস্থিত:
এখন দর্পণটির বক্রতা কেন্দ্রে একটি বস্তু \(PQ\) রাখা হল। এই \(P\) বিন্দু থেকে নির্গত একটি আলোকরশ্মি \(PA\) প্রধান অক্ষের সাথে সমান্তরাল ভাবে দর্পণের \(A\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর তা ফোকাস দিয়ে \(A{P^/}\) পথে নির্গত হয়। এবং অপর একটি আলোকরশ্মি দর্পণের বক্রতা কেন্দ্র দিয়ে লম্বভাবে \(B\) বিন্দুতে আপতিত হয়ে প্রতিফলনের পর \(B{P^/}\) পথে ফিরে যায়। এই \(A{P^/}\) এবং \(B{P^/}\) রশ্মিদুটি \({P^/}\) বিন্দুতে মিলিত হয়। এই \({P^/}\) বিন্দু থেকে প্রধান অক্ষের উপর \({P^/}{Q^/}\) লম্ব টানা হল। এখানে \({P^/}{Q^/}\) হল \(PQ\) বস্তুর সদ্ এবং অবশীর্ষ প্রতিবিম্ব।
বস্তুর অবস্থান: বক্রতা কেন্দ্রের বাইরে কিন্তু অসীমের মধ্যে।
প্রতিবিম্বের অবস্থান: ফোকাস ও বক্রতা কেন্দ্রের মধ্যেই
প্রতিবিম্বের প্রকৃতি:
(i) প্রতিবিম্বটি সদ্ হবে।
(ii) প্রতিবিম্বটি অবশীর্ষ হবে।
(iii) প্রতিবিম্বটি বস্তু অপেক্ষা ছোটো হবে।
ধরাযাক,
\(u = - x\)
\(f = - z\)
এখন গোলীয় দর্পণের সমীকরণ থেকে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{f}\)
বা, \( - \frac{1}{x} + \frac{1}{v} = - \frac{1}{z}\)
বা, \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\)
এখানে \(x > z\) তাই \(\frac{1}{x} < \frac{1}{z}\)
বা, \(\left( {\frac{1}{x} - \frac{1}{z}} \right)\) একটি ঋনাত্বক রাশি। এবং \(\frac{1}{v} = \left( {\frac{1}{x} - \frac{1}{z}} \right)\) একটি ঋনাত্বক রাশি।
বা, \(v\) ঋনাত্বক। সুতরাং প্রতিবিম্বটি দর্পণের সামনেই গঠিত হবে।
আবার \(m = - \frac{v}{u} = - \frac{{ - v}}{{ - x}} = - \frac{v}{x}\) এবং \(\left( {\frac{1}{v} - \frac{1}{x}} \right)\) একটি ধনাত্বক রাশি, তাই \(\frac{1}{v} > \frac{1}{x}\)
বা, \(v < x\)
বা, \(m = - \frac{v}{u} = - \frac{{ - v}}{{ - x}} = - \frac{v}{x}\)
বা, \(\left| m \right| < 1\)
যেহেতু \(m\) ঋনাত্বক তাই সদ্ বস্তুর সদ্ প্রতিবিম্ব গঠিত হবে এবং \(m\) ঋনাত্বক হওয়ায় প্রতিবিম্বটি অবশীর্ষ হবে এবং \(m\)<1 হওয়ায় প্রতিবিম্ব বস্তু অপেক্ষা ছোটো হবে।
বস্তু অসীমে অবস্থিত হলে:
বস্তু অসীমে অবস্থিত হলে আপতিত আলোকরশ্মি গুচ্ছ সমান্তরাল হয়। এবং এই সমান্তরাল রশ্মিগুচ্ছ প্রধান অক্ষের সমান্তরালে এসে দর্পণের উপর আপতিত হলে তা ফোকাসে মিলিত হয় অর্থাৎ প্রতিবিম্বটি ফোকাসে গঠিত হবে। এবং যদি এই সমান্তরাল রশ্মিগুচ্ছ প্রধান অক্ষের সমান্তরালে না আসে তখন ওই রশ্মিগলি ফোকাস তলেরই কোনও একটি মিলিত হবে এবং প্রতিবিম্ব গঠন করবে।
উত্তল দর্পণে গঠিত প্রতিবিম্ব:
এখানে \({M_1}O{M_2}\) উত্তল দর্পণের সামনে \(PQ\) একটি বস্তু রাখা হল। এই \(P\) বিন্দু থেকে নির্গত একটি আলোকরশ্মি \(PA\) দর্পণের প্রধান অক্ষের সমান্তরালে এসে \(AR\) পথে প্রতিফলিত হয়। এবং অপর একটি আলোকরশ্মি \(PB\) দর্পণের উপর লম্বভাবে আপতিত হয়ে \(BP\) পথেই ফিরে আসে। কোনো দর্শকের চোখে মনে হয় রশ্মিদুটি \({P^/}\) বিন্দু থেকে অপসৃত হচ্ছে। এই \({P^/}\) বিন্দু থেকে প্রধান অক্ষের উপর \({P^/}{Q^/}\) লম্ব টানা হল। এই \({P^/}{Q^/}\) হল এখানে \(PQ\) বস্তুর অসদ্ ও সমশীর্ষ প্রতিবিম্ব।
অবতল দর্পণে বস্তুর বিভিন্ন অবস্থানে গঠিত প্রতিবিম্বের অবস্থান ও প্রকৃতির তালিকা:
| বস্তুর অবস্থান | প্রতিবিম্বের অবস্থান | প্রতিবিম্বের প্রকৃতি | রৈখিক বিবর্ধন |
|---|---|---|---|
| দর্পণের মেরু O এবং ফোকাসের F এর মধ্যে | দর্পণের যেদিকে বস্তু অবস্থিত তার বিপরীতদিকে অর্থাৎ দর্পণের পিছনে | অসদ্ প্রতিবিম্ব | |
| (ii) সমশীর্ষ (iii) বিবর্ধিত | m>1 | ||
| দর্পণের ফোকাস F বিন্দুতে | বস্তু যেদিকে অবস্থিত সেদিকেই কিন্তু অসীম দূরত্বে | (i) সদ্ প্রতিবিম্ব (ii) অবশীর্ষ (iii) অনেকগুন বিবর্ধিত | m≫1 |
| দর্পণের ফোকাস F এবং বক্রতাকেন্দ্র C এর মধ্যে | বস্তু যেদিকে অবস্থিত সেদিকেই কিন্তু বক্রতাকেন্দ্র C এর থেকে বাইরের দিকে | (i) সদ্ প্রতিবিম্ব (ii) অবশীর্ষ (iii) বিবর্ধিত | m>1 |
| দর্পণের বক্রতাকেন্দ্র C তে | প্রতিবিম্বও বক্রতাকেন্দ্র C তে অবস্থিত হবে | (i) সদ্ প্রতিবিম্ব (ii) অবশীর্ষ (iii) বস্তুর আকারের সমান | m=1 |
| বক্রতাকেন্দ্র C থেকে বাইরে | দর্পণের যেদিকে বস্তু অবস্থিত সেদিকেই এবং বক্রতা ও ফোকাসের মাঝে | (i) সদ্ প্রতিবিম্ব (ii) অবশীর্ষ (iii) বস্তুর আকারের চেয়ে ছোটো | m<1 td=""> |
| অসীমে বস্তু | দর্পণের ফোকাস বিন্দু F তে | (i) সদ্ প্রতিবিম্ব (ii) বিন্দু আকার | m≪1 |
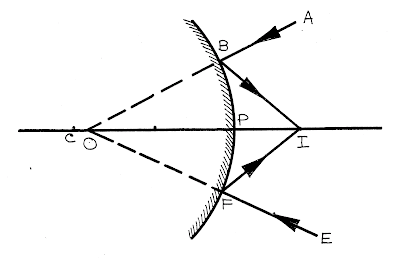
উত্তল বা অবতল দর্পণে অপসারী রশ্মিগুচ্ছের পরিবর্তে যদি অভিসারী রশ্মিগুচ্ছ আপতিত হয় তখন সেক্ষেত্রে এই অসদ্ বস্তুর সদ্ প্রতিবিম্ব গঠন করে।
যেমন, এখানে \(AB\) এবং \(EF\) আলোকরশ্মি গুচ্ছ উত্তল ও অবতল দর্পণে আপতিত হয়েছে। দর্পণটির অনুপস্থিতিতে তারা যথাক্রমে \(O\) বিন্দুতে মিলিত হতো। তাই এখানে \(O\) বিন্দু হল অসদ্বস্তু। দর্পণ দ্বারা রশ্মিগুলি প্রতিফলিত হয়ে তারা দর্পণের সামনে \(I\) বিন্দুতে মিলিত হয় এবং এখানে \(I\) হলো \(O\) অসদ্বস্তুর সদ্ প্রতিবিম্ব।
গাড়ীর চালকের পিছনে থাকা গাড়ি থেকে আগত আলোকরশ্মি গাড়ির দর্পণে আপতিত হলে, দর্পণের পিছনে থাকা ওই সমস্ত গাড়ির সমশীর্ষ এবং আকারে ছোটো প্রতিবিম্ব তৈরি হয়। এটি উত্তল দর্পণের এই দৃষ্টিক্ষেত্র অনেক বড়ো হওয়ায় গাড়ির চালক গাড়ির পিছনের বিস্তীর্ণ অঞ্চল থেকে কী কী যানবাহন আসছে তা এই দর্পণের সাহায্যে দেখতে পায়। তাই গাড়ির ভিউ ফাইন্ডার হিসাবে উত্তল দর্পণ ব্যবহার করা হয়।
অবতল দর্পণের ব্যবহার:
(i) যেহেতু অবতল দর্পণ ফোকাসের মধ্যে বস্তুর সমশীর্ষ ও বিবর্ধিত প্রতিবিম্ব গঠন করতে পারে তাই এই দর্পণকে দাড়ি কামানোর দর্পণ হিসাবে ব্যবহার করা হয়।
(ii) অবতল দর্পণের ফোকাসে অবস্থিত কোনও আলোক উৎস থেকে নিঃসৃত আলোকরশ্মি গুচ্ছ প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছ রূপে প্রতিফলিত হয় বলে এই দর্পণকে সার্চলাইটের প্রতিফলক, মোটর গাড়ির হেড লাইটের প্রতিফলক তল ও সৌর চুল্লিতে ব্যবহার করা হয়।
(iii) দাঁত ও গলার ভিতরের অংশ দেখার জন্য চিকিৎসকেরা এই অবতল দর্পণ ব্যবহার করেন।
(iv) রেটিনাতে আলো ফেলার জন্য চক্ষু চিকিৎসকেরা অপথালমোস্কোপে অবতল দর্পণ ব্যবহার করেন।
উত্তল দর্পণের ব্যবহার:
(i) উত্তল দর্পণ সর্বদা সমশীর্ষ বস্তু থেকে ক্ষুদ্রতর প্রতিবিম্ব গঠন করায় এবং এর দৃষ্টিক্ষেত্র অনেক বড়ো হওয়ায় এই দর্পণকে মোটর গাড়ীর চালকের সামনে ভিউ ফাইন্ডার হিসাবে ব্যবহার করা হয়। তার ফলে গাড়ির চালক এই দর্পণের মাধ্যমে পিছনের সকল বস্তুকে দেখতে পায়।
(ii) উত্তল দর্পণ আলোকে বিস্তীর্ণ অঞ্চলে ছড়িয়ে দিতে পারে বলে, এই দর্পণকে রাস্তার বাতির প্রতিফলক হিসাবে ব্যবহার করা হয়।
একটি সমতল দর্পণের বক্রতা ব্যাসার্ধ্য \( = \infty \)
তাই সমতল দর্পণের ফোকাস দূরত্বও হবে \(\infty \)
এখন গোলীয় দর্পণের সমীকরণে বক্রতা ব্যসার্ধ্য \(\infty \) বসিয়ে পাই,
\(\frac{1}{u} + \frac{1}{v} = \frac{1}{\infty } = 0\)
বা, \(u = - v\)
অর্থাৎ বস্তুদূরত্ব ও প্রতিবিম্ব দূরত্ব সমান এবং বস্তু ও প্রতিবিম্ব বিপরীত পার্শ্বে অবস্থিত হয় এবং প্রতিবিম্বটি অসদ্ হয়।
একটি সমতল দর্পণে রৈখিক বিবর্ধনের মান কত?
সমতল দর্পণে গঠিত প্রতিবিম্ব, বস্তুর আকারের সমান হয়। তাই \({h_o} = {h_i}\)
সুতরাং রৈখিক বিবর্ধন (\(m\)): \( = \frac{{{h_o}}}{{{h_i}}} = 1\) হয়।
কোন্ ধরণের দর্পণে ফোকাস দূরত্ব অসীম হয়?
সমতল দর্পণের ফোকাস দূরত্ব অসীম হয়।
COMMENTS