Maximize your chance of success and high rank in JEE (Main & Advance), WBJEE, NEET. This notes specially designed column is updated year after year by a panel of highly qualified teaching expert well tuned to that Entrance Examination, Electrostatics, Electric Electric Force & Field, Electric Potential
The strength of particle's electric interaction with object around it depends on its electric charge, which can be either positive or negative. An object with equal amounts of the two kinds of charge is electrically neutral, whereas one with an imbalance is electrically charged.
In the table given below, if a body in the first column is rubbed against a body in the second column, the body in the first column will acquire positive charge, while that in the second column will acquire negative charge.
| SL No. | First Column | Second Column |
|---|---|---|
| 1 | Glass rod | Silk rod |
| 2 | Flannes or cat skin | Ebonite rod |
| 3 | Woolen cloth | Amber |
| 4 | Woolen cloth | Rubber shoe |
| 5 | Woolen cloth | Plastic objects |
Electric charge and its properties:
(1) Charge is a basic property associated with the elementary particles. It is scalar quantity.
(2) Elementary charge (e) is one of the fundamental constant with the value, value, \(e = - 1.602 \times {10^{ - 19}}C\)
(3) There are two kind of charges, positive and negative.
(4) Mass, length and time depend on state of rest or motion while charge is invariant (theory of relativity).
(5) Electric charge is quantised. i.e. \(q = ne\) where, \(n = 0, \pm 1, \pm 2, \pm 3,......\)
(6) The charge of an isolated system is conserved.
(7) Amount of induced charge \( \le \) inducing charge, sign of equality holds only for metals.
Coulomb's law and Factor Affecting it:
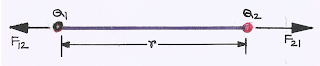 |
| Coulomb's Law |
(1) Coulomb's law, \(F = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\), where, \(\frac{1}{{4\pi {\varepsilon _0}}} = 9 \times {10^9}N{m^2}{C^{ - 2}}\)
Here, (i) \(\overrightarrow {{F_{12}}} = - \overrightarrow {{F_{21}}} \)
(ii) \({F_{12}} = {F_{21}} = F\)
(2) Electric force between two charges does not depend on neighboring charges.
(3) If a dielectric slab (\({ \in _r}\)) of thickness is placed between two charges kept at a distance then the electric force decreases. This reduce force is given by
(4) If for two identical charges, then \(F = \frac{1}{{4\pi { \in _0}}}\frac{{{Q_1}{Q_2}}}{{{r^2}}}\) where, \(r = d - t + t\sqrt {{ \in _r}} \)
(5) If \({F_g} = {F_e}\) for two identical charges, then \(\frac{Q}{m} = \sqrt {4\pi { \in _0}G} \)
(6) When two charges \({Q_1}\) and \({Q_2}\) are placed some distance apart, neutral point is nearer to smaller charge and in between \({Q_1}\) and \({Q_2}\) if charges are alike.
(1) Coulomb's law is only applicable for point charges.
(2) Like charged bodies may attract each other
(3) Attraction also takes place between charged and neutral body.
(4) Electrostatics force of attraction in conservative in nature.
(5) The work done by electrostatics force does not depends upon path. It only depends upon initial and final positions.
(6) In a closed path work done by electrostatics force is zero i.e., \(\int\limits_c {\overrightarrow F .\overrightarrow {dl} = 0} \)
(7) Coulomb's law holds good for all distance greater than \({10^{ - 15}}m\)
(8) No relativistic variation is found in electric charge.
(9) The transfer of charge without mass is not possible.
(10) The transfer of mass without charge is possible.
(11) Massless particle (e.g., photon) never be charged.
(12) Charging by induction takes place without any loss of charge from the charging body.
(13) The magnitude of induced charged is always less or equal to charging body.
(14) Electrostatics induction only takes place between bodies of definite shape (either conducting or non-conducting)
Electric field:
Electric Field Intensity in Some Particular Cases:
\(Ch\arg e \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} Electric - Field \mathbin{\lower.3ex\hbox{$\buildrel\textstyle\rightarrow\over{\smash{\leftarrow}\vphantom{_{\vbox to.5ex{\vss}}}}$}} Ch\arg e\)
First charge sets up an electric field and the second charge interacts with the electric field of the first charge.
(1) \(\overrightarrow E = \frac{{\overrightarrow F }}{{{q_0}}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}}\hat r\)
The direction of \(\overrightarrow E \) is the same as the direction of \(\overrightarrow F \) because the test charge \({q_0}\) is a positive scalar quantity.
(2) Electric force on a charge in a uniform electric field (\(E\)) is constant hence acceleration is constant, so equation of motion can be used (acceleration ) \(a = \frac{{qE}}{m}\)
Isolated Charge:
 |
| Electric Field Due to a Point Charge |
\(E = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}}\hat r\)
Potential, \(V = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r}\)
Potential, \(V = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r}\)
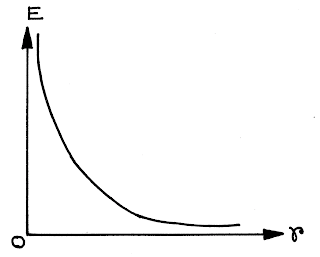 |
| Variation of Electric Field with Distance |
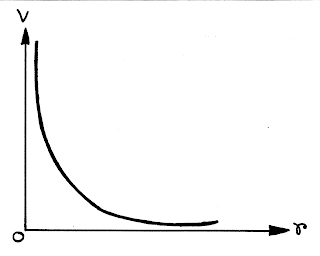 |
| Variation of Potential with Distance |
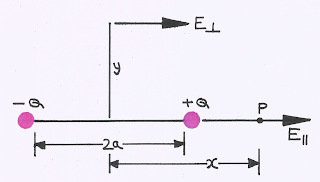
\(\overrightarrow {{E_\parallel }} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{2\overrightarrow p }}{{{x^3}}}\)
\({\overrightarrow E _ \bot } = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{\overrightarrow p }}{{{y^3}}}\)
\(E = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{p\sqrt {3{{\cos }^2}\theta + 1} }}{{{r^3}}}\)
A Charged Ring:
For a charged ring of radius \(R\)
 |
| Field due to Charge Ring |
 |
| Variation of Electric Field along the axis of the Ring |
\({E_P} = \frac{{KQx}}{{{{\left( {{R^2} + {x^2}} \right)}^{\frac{3}{2}}}}}\)
(1) If \(x \gg R\) then, \({E_p} = \frac{{KQ}}{{{x^2}}}\)
(2) If \(x \ll R\) then, \({E_P} = \frac{{kQx}}{{{R^3}}}\)
(3) As \(x\) increases Electric field \(\overrightarrow E \) due to ring first increses then decreases and at \(x = \pm \frac{R}{{\sqrt 2 }}\) it is maximum.
A Charged Disc:
\(E = \frac{\sigma }{{2{\varepsilon _0}}}\left[ {1 - \frac{x}{{\sqrt {{x^2} + {R^2}} }}} \right]\)
An Infinite sheet of Charge:
\(E = \frac{\sigma }{{2{\varepsilon _0}}}\)
Here we noted that, \(E \propto {r^0}\) and
Potential \(V = - \frac{{\sigma r}}{{2{\varepsilon _0}}} + C\)
Electric Field Due To Two Parallel Plane Sheet of Charged:
Consider two large, uniformly charged parallel plates A and B having surface charge densities are \({\sigma _A}\) and \({\sigma _B}\) respectively. Suppose net electric field at point P, Q and R is to be calculated,
At P, \({E_P} = \left( {{E_A} + {E_B}} \right) = \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} + {\sigma _B}} \right)\)
At Q, \({E_Q} = \left( {{E_A} - {E_B}} \right) = \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} - {\sigma _B}} \right)\)
At R, \({E_R} = - \left( {{E_A} + {E_B}} \right) = - \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} + {\sigma _B}} \right)\)
If, \({\sigma _A} = + \sigma \) and, \({\sigma _B} = - \sigma \) then,
\({E_P} = {E_R} = 0\) and \({E_Q} = \frac{\sigma }{{{\varepsilon _0}}}\)
Thus in case of two infinite plane sheet of charge having equal and opposite surface charge densities, the field in non-zero only in the space between the two sheet and is independent of the distance between them, i.e., field is uniform in this region.
Conducting Sheet of Charge:
\(E = \frac{\sigma }{{{\varepsilon _0}}}\) and
\(V = - \frac{{\sigma r}}{{{\varepsilon _0}}} + C\)
An Infinite Long Line of Charge:
\(E = \frac{\lambda }{{2\pi {\varepsilon _0}r}}\)
A Finite Line of Charge:
\({E_ \bot } = \frac{\lambda }{{4\pi {\varepsilon _0}x}}\left( {\sin \alpha + \sin \beta } \right)\)
\({E_\parallel } = \frac{\lambda }{{4\pi {\varepsilon _0}x}}\left( {\cos \alpha - \cos \beta } \right)\)
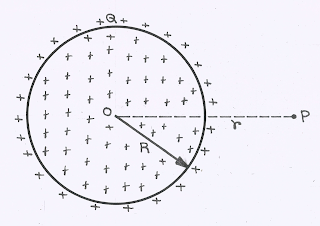
Charged Spherical Shell or Charged Solid Conducting Sphere (Surface Charge Distribution):
(1) Outside the Sphere/Shell:
Here \(P\) is a point outside the sphere at a distance \(r\) from the centre at which electric field and potential is to be determined.
Electric Field at \(P\),
\({E_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}} = \frac{{\sigma {R^2}}}{{{\varepsilon _0}{r^2}}}\) and,
\({V_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r} = \frac{{\sigma {R^2}}}{{{\varepsilon _0}r}}\)
(2) At The Surface of The Sphere/Shell:
At Surface, \(r = R\)
So, \({E_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{R^2}}} = \frac{\sigma }{{{\varepsilon _0}}}\) and,
\({V_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{{\sigma R}}{{{\varepsilon _0}}}\)
(3) Inside of The Shell/Sphere:
Inside the conducting charged sphere, electric field is zero and potential remains constant every where and equal to the potential at the surface.
\(0 < r < R\), \({E_{in}} = 0\) and \({V_{in}} = cons. = {V_S}\)
Solid Non-Conducting Sphere of Charge (Volume Charge Distribution):
Charge given to a non-conducting spheres spreads uniformly throughout its volume.
(1) Outside The Sphere at \(P\):
\({E_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}}\) and \({V_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r}\)
By Using, \(\rho = \frac{Q}{{\frac{4}{3}\pi {R^3}}}\) we get,
\({E_{out}} = \frac{{\rho {R^3}}}{{3{\varepsilon _0}{r^2}}}\) and \({V_{out}} = \frac{{\rho {R^3}}}{{3{\varepsilon _0}r}}\)
(2) At Surface of The Sphere:
At surface, \(r = R\)
\({E_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{R^2}}} = \frac{{\rho R}}{{3{\varepsilon _0}}}\) and \({V_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{{\rho {R^2}}}{{3{\varepsilon _0}}}\)
(3) Inside The Sphere:
At a distance \(r\) from the centre
\({E_{in}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qr}}{{{R^3}}} = \frac{{\rho r}}{{3{\varepsilon _0}}}\), Here, \({E_{in}} \propto r\) and \({V_{in}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Q\left( {3{R^2} - {r^2}} \right)}}{{2{R^3}}} = \frac{{\rho \left( {3{R^2} - {r^2}} \right)}}{{6{\varepsilon _0}}}\)
(4) At the centre \(r = 0\), So \({V_{centre}} = \frac{3}{2} \times \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{3}{2}{V_S}\)
Therefore, \({V_{centre}} > {V_{surface}} > {V_{out}}\)
A Charged Disc:
 |
| A disc of Charge |
An Infinite sheet of Charge:
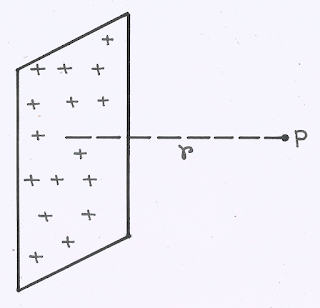 |
| A Charged Infinite Sheet |
Here we noted that, \(E \propto {r^0}\) and
Potential \(V = - \frac{{\sigma r}}{{2{\varepsilon _0}}} + C\)
Electric Field Due To Two Parallel Plane Sheet of Charged:
![[feature] Electrostatics, Electric Field Electrostatics, Electric Field](https://blogger.googleusercontent.com/img/b/R29vZ2xl/AVvXsEhOmS4yBmj8uyTtH4FLe0SqE7EZuFzRho_afk223pJWRPxYY-2EwIa22S6x78NXcCgtdRsXvr29ntnKH-991kdYSMSdxODf294UR2JAwQ1CToEl9jSXVAfT7qXKjTKHy5XZ6UvFVIMP5H67/s320/10.png) |
| Two Parallel Plane Charged Sheet |
At P, \({E_P} = \left( {{E_A} + {E_B}} \right) = \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} + {\sigma _B}} \right)\)
At Q, \({E_Q} = \left( {{E_A} - {E_B}} \right) = \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} - {\sigma _B}} \right)\)
At R, \({E_R} = - \left( {{E_A} + {E_B}} \right) = - \frac{1}{{2{\varepsilon _0}}}\left( {{\sigma _A} + {\sigma _B}} \right)\)
If, \({\sigma _A} = + \sigma \) and, \({\sigma _B} = - \sigma \) then,
\({E_P} = {E_R} = 0\) and \({E_Q} = \frac{\sigma }{{{\varepsilon _0}}}\)
Thus in case of two infinite plane sheet of charge having equal and opposite surface charge densities, the field in non-zero only in the space between the two sheet and is independent of the distance between them, i.e., field is uniform in this region.
Conducting Sheet of Charge:
 |
| Conducting Sheet of Charge |
\(V = - \frac{{\sigma r}}{{{\varepsilon _0}}} + C\)
An Infinite Long Line of Charge:
 |
| An infinite long Charged wire |
A Finite Line of Charge:
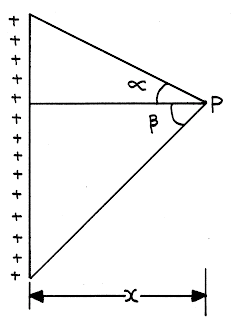 |
| A finite long Charged Wire |
\({E_\parallel } = \frac{\lambda }{{4\pi {\varepsilon _0}x}}\left( {\cos \alpha - \cos \beta } \right)\)
Charged Spherical Shell or Charged Solid Conducting Sphere (Surface Charge Distribution):
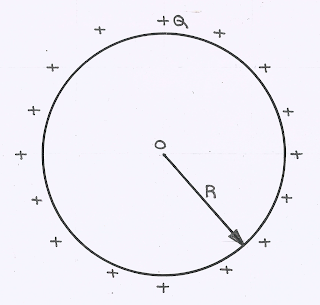 |
| Solid Charged Conducting Sphere |
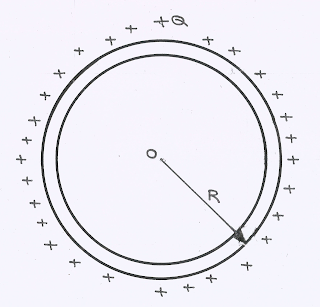 |
| Charged Conducting Shell |
 |
| Variation of Electric Field With Distance |
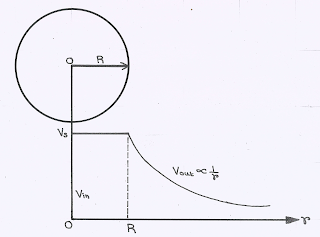 |
| Variation of Potential With Distance |
Here \(P\) is a point outside the sphere at a distance \(r\) from the centre at which electric field and potential is to be determined.
Electric Field at \(P\),
\({E_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}} = \frac{{\sigma {R^2}}}{{{\varepsilon _0}{r^2}}}\) and,
\({V_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r} = \frac{{\sigma {R^2}}}{{{\varepsilon _0}r}}\)
(2) At The Surface of The Sphere/Shell:
At Surface, \(r = R\)
So, \({E_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{R^2}}} = \frac{\sigma }{{{\varepsilon _0}}}\) and,
\({V_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{{\sigma R}}{{{\varepsilon _0}}}\)
(3) Inside of The Shell/Sphere:
Inside the conducting charged sphere, electric field is zero and potential remains constant every where and equal to the potential at the surface.
\(0 < r < R\), \({E_{in}} = 0\) and \({V_{in}} = cons. = {V_S}\)
Solid Non-Conducting Sphere of Charge (Volume Charge Distribution):
 |
| Charged Non-Conducting Sphere |
 |
| Variation of Electric Field with Distance |
 |
| Variation of Potential with Distance |
(1) Outside The Sphere at \(P\):
\({E_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{r^2}}}\) and \({V_{out}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{r}\)
By Using, \(\rho = \frac{Q}{{\frac{4}{3}\pi {R^3}}}\) we get,
\({E_{out}} = \frac{{\rho {R^3}}}{{3{\varepsilon _0}{r^2}}}\) and \({V_{out}} = \frac{{\rho {R^3}}}{{3{\varepsilon _0}r}}\)
(2) At Surface of The Sphere:
At surface, \(r = R\)
\({E_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{{{R^2}}} = \frac{{\rho R}}{{3{\varepsilon _0}}}\) and \({V_S} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{{\rho {R^2}}}{{3{\varepsilon _0}}}\)
(3) Inside The Sphere:
At a distance \(r\) from the centre
\({E_{in}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Qr}}{{{R^3}}} = \frac{{\rho r}}{{3{\varepsilon _0}}}\), Here, \({E_{in}} \propto r\) and \({V_{in}} = \frac{1}{{4\pi {\varepsilon _0}}}\frac{{Q\left( {3{R^2} - {r^2}} \right)}}{{2{R^3}}} = \frac{{\rho \left( {3{R^2} - {r^2}} \right)}}{{6{\varepsilon _0}}}\)
(4) At the centre \(r = 0\), So \({V_{centre}} = \frac{3}{2} \times \frac{1}{{4\pi {\varepsilon _0}}}\frac{Q}{R} = \frac{3}{2}{V_S}\)
Therefore, \({V_{centre}} > {V_{surface}} > {V_{out}}\)
















COMMENTS