Mechanics: The branch of a physics that deals with the motion of a body due to the application of force is called Mechanics. Statics...
Mechanics:
The branch of a physics that deals with the motion of a body due to the application of force is called Mechanics.
Statics:
The branch of mechanics that deals with the state of rest of a body is called statics.
Dynamics:
The branch of mechanics that deals with the state of motion of a body is called dynamics.
Kinematics:
Kinematics is the study of motion which relates to the motion of bodies without reference to either the mass or the force causing it.
Kinetics:
Kinetics is the study of motion which relates to the action of force causing the motion and the mass is involved.
Position:
Position of any point is completely expressed by two factors. Its distance from the observer and its direction with with respect to the observer. Position of a particle is characterized by a vector known as position vector.
Let o point P is in XY plane and its co-ordinates are (x, y). Then position vector \(\overrightarrow r \) of the point will be \(\overrightarrow r = x\hat i + y\hat j\) and if the point P is in a space and its co-ordinates are (x, y, z), then position vector can be expressed as \(\overrightarrow r = x\hat i + y\hat j + z\hat k\)
Time:
It is the measure of succession of events. It is a scalar quantity. If any event is started at \(t = 0\), then time will not be negative. But is the observation is started after the start of event then time may negative.
Rest and Motion:
If a body does not change its position as time passes with respect to frame of reference, it is said to be at rest. And if a body changes its position as time passes with respect to frame of reference, it is said to be in motion. Rest and motion are relative terms. It depends upon the frame of reference.
Frame of Reference:
It is a system to which a set of co-ordinates are attached and with reference to which observer describes any events.
Inertial Frame of Reference:
(i) Here all Newton's law hold good.
(ii) The motion of the particles appears un-accelerated. The frame of reference is un-accelerated.
(iii) The particles moves with a constant velocity in the absence of external force.
Non-inertial Frame of Reference:
(i) Newton's Law of motion does not hold good.
(ii) The motion of the particles appears accelerated.
(iii) In this frame, the particles does not move with constant velocity.
(iv) An object is said to be in motion if it changes its position with time, with respect to its surroundings.
Types of Motion:
Particle or Point Mass:
The smallest part of the matter with zero dimension which can be described by its mass and position is defined as a particle. If the size of a body is negligible in comparison to its range of motion, then that body is known as a particle. When we treat a body as particle, all parts of the body undergo same displacement and have same velocity and acceleration.
Distance & Displacement:
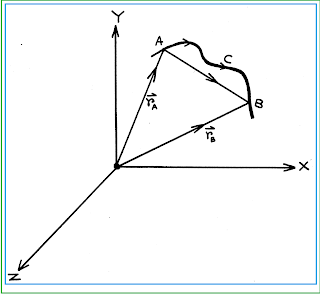
Suppose an insect is at point A (\({x_1},{y_1},{z_1}\)) at \(t = {t_1}\). It reaches at point B (\({x_2},{y_2},{z_2}\)) at \(t = {t_2}\) through the path ACB with respect to the frame shown in figure. The actual length of curved path ACB is the distance travelled by the insect in time \(\Delta t = \left( {{t_2} - {t_1}} \right)\).
If we connect the point A (initial point) and point B (final point) by a straight line, then the length of straight line AB gives the magnitude of displacement of insect in time interval \(\Delta t = {t_2} - {t_1}\). The direction of displacement is directed from A to B through the straight line AB.
From the concept of vector of \(\overrightarrow A \) is \(\overrightarrow {{r_A}} = {x_1}\hat i + {y_1}\hat j + {z_1}\hat k\) and that of \(\overrightarrow B = {x_2}\hat i + {y_2}\hat j + {z_2}\hat k\).
According to addition law of vectors,
\(\overrightarrow {{r_A}} = \overrightarrow {AB} + \overrightarrow {{r_B}} \)
or, \(\overrightarrow {AB} = \overrightarrow {{r_B}} - \overrightarrow {{r_A}} \)
or, \(\overrightarrow {AB} = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j + \left( {{z_2} - {z_1}} \right)\hat k\)
The magnitude of displacement is
\(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} \)
Comparison between distance and displacement:
(1) The magnitude of displacement is equal to minimum possible distance between two positions. So, Distance \( \ge \) \(\left| {displacement} \right|\)
(2) For a moving particle distance can never be negative or zero while displacement can be. That is, Distance > 0, but Displacement > or = or < zero (0)
(3) For motion between two points, displacement is single valued while distance depends on actual path and so can have many values.
(4) For a moving particle distance can never decreases with time while displacement can. Decrease in displacement with time means body is moving towards the initial position.
(5) In general magnitude of displacement is not equal to distance. However, it can be so if the motion is along a straight line without change in direction.
(6) If \(\overrightarrow {{r_A}} \) and \(\overrightarrow {{r_B}} \) are the position vectors of a particle initially and finally, then the displacement of the particle is \(\overrightarrow {{r_{AB}}} = \overrightarrow {{r_B}} - \overrightarrow {{r_A}} \), and S is the distance travelled if the particle has gone through the path ACB.
Some Conceptual Points:
(1) Distance is a scalar quantity.
(2) Distance never be negative.
(3) For moving body, distance is always greater than zero.
(4) Distance never be equal to displacement.
(5) Displacement is a vector quantity.
(6) If a body is moving continuously in a given direction on a straight line, then the magnitude of displacement is equal to distance.
(7) Generally, the magnitude of displacement is less or equal to distance.
(8) Many paths are possible between two points. For different paths between two points, distance are different but magnitude of displacement are same.
(9) The slope of distance-time graph is always greater or equal to zero.
(10) The slope of displacement-time graph may be negative.
Speed:
Rate of distance covered with time is called speed.
(1) It is scalar quantity having symbol \(v\)
(2) Dimension: \(\left[ {{M^0}{L^1}{T^{ - 1}}} \right]\)
(3) In S.I. System its unit is m/s and in C.G.S system its unit is cm/s
(4) Types of Speed:
Uniform Speed:
When a particle covers equal distances in equal interval of time, then it is said to be moving with uniform speed.
Non-uniform Speed:
In non-uniform speed a particle covers unequal distance in equal interval of time.
Average Speed:
The average speed of a particle for a given 'interval of time' is defined as the ratio of the total distance travelled to the time taken.
Average speed = \(\frac{{Distance\_travelled}}{{Time\_taken}}\)
or, \({v_{av}} = \frac{{\Delta S}}{{\Delta t}}\)
Average Speed are basically two types: (1) Time average speed (ii) Distance average speed.
Time Average Speed:
When a particle moves with different uniform speed \({v_1},{v_2},{v_3}...\) etc in different time intervals \({t_1},{t_2},{t_3}...\) etc respectively, its average speed over the total time of journey is given as
\({v_{av}} = \frac{{Total\_dis\tan ce\_{\mathop{\rm cov}} ered}}{{Total\_time\_elapsed}} = \frac{{{d_1} + {d_2} + {d_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}} = \frac{{{v_1}{t_1} + {v_2}{t_2} + {v_3}{t_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}}\)
Special Cases: When a particle moves with speed with speed \({v_1}\) upto halftime of its total motion and in rest time it is moving with speed \({v_2}\) then \({v_{av}} = \frac{{{v_1} + {v_2}}}{2}\)
Distance Average Speed:
When a particle describes different distances \({d_1},{d_2},{d_3}...\) with different time intervals \({t_1},{t_2},{t_3},...\) with speeds \({v_1},{v_2},{v_3},...\) respectively then the speed of particles averaged over the total distance can be given as
\({v_{av}} = \frac{{Total - Distance - {\mathop{\rm cov}} ered}}{{Total - time - elapsed}} = \frac{{{d_1} + {d_2} + {d_3} + ...}}{{{t_1} + {t_2} + {t_3} + ..}} = \frac{{{v_1}{t_1} + {v_2}{t_2} + {v_3}{t_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}}\)
Special Cases:
When a particle moves the first half of a speed of \({v_1}\) and second half of the distance at speed \({v_2}\) then, \({v_{av}} = \frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)
When a particle covers one third distance at speed \({v_1}\), next one third at speed \({v_2}\) and last one third at speed \({v_3}\), then, \({v_{av}} = \frac{{3{v_1}{v_2}{v_3}}}{{{v_1}{v_2} + {v_2}{v_3} + {v_1}{v_3}}}\)
Instantaneous Speed:
It is the speed of a particle at particular instant. When we say "speed", it usually means instantaneous speed.
The instantaneous speed is average speed for infinitesimally small time interval (\(\Delta t \to 0\)). Thus, instantaneous speed \(v = \mathop {\lim }\limits_{\Delta t \to \infty } \frac{{\Delta S}}{{\Delta t}} = \frac{{dS}}{{dt}}\)
Velocity:
Rate of change of position in a particular direction i.e., rate of displacement with time is called velocity.
(1) It is a vector quantity.
(2) Dimension: \(\left[ {{M^0}{L^1}{T^{ - 1}}} \right]\)
(3) In S.I system, Its unit is m/sec and in C.G.S system its unit is cm/sec
(4) Types:
Uniform Velocity:
A particle is said to have uniform velocity, if magnitude as well as direction of its velocity remains same and this is possible only when the particle moves in same straight line without changing its direction.
Non-uniform Velocity:
A particle is said to have non-uniform velocity, if either of magnitude or direction or both are changed.
Average Velocity:
It is defined as the ratio of displacement to time taken by the body. \(\overrightarrow {{v_{av}}} = \frac{{\overrightarrow {\Delta r} }}{{\Delta t}}\)
Instantaneous Velocity:
Instantaneous velocity is defined as rate of change of position vector of particles with time ar a certain instant of time.
Instantaneous velocity = \(\overrightarrow v = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \overrightarrow r }}{{\Delta t}} = \frac{{dr}}{{dt}}\)
If position of a particle at an instant \(t\) is \(\overrightarrow r = x\hat i + y\hat j + z\hat k\), Then,
x component of velocity is \({v_x} = \frac{{dx}}{{dt}}\)
y component of velocity is \({v_y} = \frac{{dy}}{{dt}}\)
z component of velocity is \({v_z} = \frac{{dz}}{{dt}}\)
Thus, The velocity of the particle is, \(v = {v_x}\hat i + {v_y}\hat j + {v_z}\hat k\) = \(\frac{{dx}}{{dt}}\hat i + \frac{{dy}}{{dt}}\hat j + \frac{{dz}}{{dt}}\hat k\)
Some Important Point:
(1) Average velocity may or may not be equal to instantaneous velocity.
(2) If body moves with constant velocity, the instantaneous velocity is equal to average velocity.
(3) The instantaneous speed is equal to modulus of instantaneous velocity.
(4) Distance travelled by the particle is \(S = \int {\left| {\overrightarrow v } \right|dt} \)
(5) \(x\) component of displacement is \(\Delta x = \int {{v_x}dt} \)
\(y\) component of displacement is \(\Delta y = \int {{v_y}dt} \)
\(z\) component of displacement is \(\Delta z = \int {{v_z}dt} \)
Thus, displacement of particle is \(\overrightarrow {\Delta r} = \Delta x\hat i + \Delta y\hat j + \Delta z\hat k\)
(6) If particle moves on a straight line (along X axis), then, \(\overrightarrow v = \frac{{d\overrightarrow x }}{{dt}}\)
(7) The area of velocity-time graph gives displacement.
(8) The area of speed-time graph gives distance.
(9) The slope of tangent at position-time graph at a particular instant gives instantaneous velocity at that instant.
Comparison between instantaneous speed and instantaneous velocity:
(1) Instantaneous velocity is always tangential to the path followed by the particle. When a stone is thrown from a point O then, at point of projection the instantaneous velocity of stone is \({v_1}\), at point A the instantaneous velocity of stone is \({v_2}\), similarly at point B and C are \({v_3}\) and \({v_4}\) respectively. Direction of these velocities can be found out by drawing a tangent on the trajectory at o given point.
(2) A particle may have constant instantaneous speed but variable instantaneous velocity. When a particle is performing uniform circular motion then for every instant of its circular motion its speed remains constant but velocity change at every instant.
(3) The magnitude of instantaneous velocity is equal to the instantaneous speed.
(4) If a particle is moving with constant velocity then, its average velocity and instantaneous velocity are always equal.
(5) If displacement is given as a function of time, then time derivative of displacement will give velocity.
Comparison between average speed and average velocity:
Position:
Position of any point is completely expressed by two factors. Its distance from the observer and its direction with with respect to the observer. Position of a particle is characterized by a vector known as position vector.
Let o point P is in XY plane and its co-ordinates are (x, y). Then position vector \(\overrightarrow r \) of the point will be \(\overrightarrow r = x\hat i + y\hat j\) and if the point P is in a space and its co-ordinates are (x, y, z), then position vector can be expressed as \(\overrightarrow r = x\hat i + y\hat j + z\hat k\)
Time:
It is the measure of succession of events. It is a scalar quantity. If any event is started at \(t = 0\), then time will not be negative. But is the observation is started after the start of event then time may negative.
If a body does not change its position as time passes with respect to frame of reference, it is said to be at rest. And if a body changes its position as time passes with respect to frame of reference, it is said to be in motion. Rest and motion are relative terms. It depends upon the frame of reference.
Frame of Reference:
It is a system to which a set of co-ordinates are attached and with reference to which observer describes any events.
(i) Here all Newton's law hold good.
(ii) The motion of the particles appears un-accelerated. The frame of reference is un-accelerated.
(iii) The particles moves with a constant velocity in the absence of external force.
Non-inertial Frame of Reference:
(i) Newton's Law of motion does not hold good.
(ii) The motion of the particles appears accelerated.
(iii) In this frame, the particles does not move with constant velocity.
(iv) An object is said to be in motion if it changes its position with time, with respect to its surroundings.
Types of Motion:
| One Dimensional | Two Dimensional | Three Dimensional |
|---|---|---|
| Motion of body in a straight line is called one dimensional motion. | Motion of body in a plane is called two dimensional motion. | Motion of a body in space is called three dimensional motion. |
| When only co-ordinates of the position of a body change with time then it is said to be moving one dimensionally. | When two co-ordinates of the position of a body changes with time then it is said to be moving two dimensionally. | When all three co-ordinates of the position of a body changes with time then it is said to be moving three dimensionally. |
| Motion of car on a straight road. Motion of freely falling body. | Motion of a car on a circular turn. Motion of billiard ball. | Motion of a flying kite. Motion of a insect. |
Particle or Point Mass:
The smallest part of the matter with zero dimension which can be described by its mass and position is defined as a particle. If the size of a body is negligible in comparison to its range of motion, then that body is known as a particle. When we treat a body as particle, all parts of the body undergo same displacement and have same velocity and acceleration.
Distance & Displacement:
Suppose an insect is at point A (\({x_1},{y_1},{z_1}\)) at \(t = {t_1}\). It reaches at point B (\({x_2},{y_2},{z_2}\)) at \(t = {t_2}\) through the path ACB with respect to the frame shown in figure. The actual length of curved path ACB is the distance travelled by the insect in time \(\Delta t = \left( {{t_2} - {t_1}} \right)\).If we connect the point A (initial point) and point B (final point) by a straight line, then the length of straight line AB gives the magnitude of displacement of insect in time interval \(\Delta t = {t_2} - {t_1}\). The direction of displacement is directed from A to B through the straight line AB.
From the concept of vector of \(\overrightarrow A \) is \(\overrightarrow {{r_A}} = {x_1}\hat i + {y_1}\hat j + {z_1}\hat k\) and that of \(\overrightarrow B = {x_2}\hat i + {y_2}\hat j + {z_2}\hat k\).
According to addition law of vectors,
\(\overrightarrow {{r_A}} = \overrightarrow {AB} + \overrightarrow {{r_B}} \)
or, \(\overrightarrow {AB} = \overrightarrow {{r_B}} - \overrightarrow {{r_A}} \)
or, \(\overrightarrow {AB} = \left( {{x_2} - {x_1}} \right)\hat i + \left( {{y_2} - {y_1}} \right)\hat j + \left( {{z_2} - {z_1}} \right)\hat k\)
The magnitude of displacement is
\(\left| {\overrightarrow {AB} } \right| = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2} + {{\left( {{z_2} - {z_1}} \right)}^2}} \)
Comparison between distance and displacement:
(2) For a moving particle distance can never be negative or zero while displacement can be. That is, Distance > 0, but Displacement > or = or < zero (0)
(3) For motion between two points, displacement is single valued while distance depends on actual path and so can have many values.
(4) For a moving particle distance can never decreases with time while displacement can. Decrease in displacement with time means body is moving towards the initial position.
(5) In general magnitude of displacement is not equal to distance. However, it can be so if the motion is along a straight line without change in direction.
(6) If \(\overrightarrow {{r_A}} \) and \(\overrightarrow {{r_B}} \) are the position vectors of a particle initially and finally, then the displacement of the particle is \(\overrightarrow {{r_{AB}}} = \overrightarrow {{r_B}} - \overrightarrow {{r_A}} \), and S is the distance travelled if the particle has gone through the path ACB.
Some Conceptual Points:
(1) Distance is a scalar quantity.
(2) Distance never be negative.
(3) For moving body, distance is always greater than zero.
(4) Distance never be equal to displacement.
(5) Displacement is a vector quantity.
(6) If a body is moving continuously in a given direction on a straight line, then the magnitude of displacement is equal to distance.
(7) Generally, the magnitude of displacement is less or equal to distance.
(8) Many paths are possible between two points. For different paths between two points, distance are different but magnitude of displacement are same.
(9) The slope of distance-time graph is always greater or equal to zero.
(10) The slope of displacement-time graph may be negative.
Speed:
Rate of distance covered with time is called speed.
(1) It is scalar quantity having symbol \(v\)
(2) Dimension: \(\left[ {{M^0}{L^1}{T^{ - 1}}} \right]\)
(3) In S.I. System its unit is m/s and in C.G.S system its unit is cm/s
(4) Types of Speed:
Uniform Speed:
When a particle covers equal distances in equal interval of time, then it is said to be moving with uniform speed.
Non-uniform Speed:
In non-uniform speed a particle covers unequal distance in equal interval of time.
Average Speed:
The average speed of a particle for a given 'interval of time' is defined as the ratio of the total distance travelled to the time taken.
Average speed = \(\frac{{Distance\_travelled}}{{Time\_taken}}\)
or, \({v_{av}} = \frac{{\Delta S}}{{\Delta t}}\)
Average Speed are basically two types: (1) Time average speed (ii) Distance average speed.
Time Average Speed:
When a particle moves with different uniform speed \({v_1},{v_2},{v_3}...\) etc in different time intervals \({t_1},{t_2},{t_3}...\) etc respectively, its average speed over the total time of journey is given as
\({v_{av}} = \frac{{Total\_dis\tan ce\_{\mathop{\rm cov}} ered}}{{Total\_time\_elapsed}} = \frac{{{d_1} + {d_2} + {d_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}} = \frac{{{v_1}{t_1} + {v_2}{t_2} + {v_3}{t_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}}\)
Special Cases: When a particle moves with speed with speed \({v_1}\) upto halftime of its total motion and in rest time it is moving with speed \({v_2}\) then \({v_{av}} = \frac{{{v_1} + {v_2}}}{2}\)
Distance Average Speed:
When a particle describes different distances \({d_1},{d_2},{d_3}...\) with different time intervals \({t_1},{t_2},{t_3},...\) with speeds \({v_1},{v_2},{v_3},...\) respectively then the speed of particles averaged over the total distance can be given as
\({v_{av}} = \frac{{Total - Distance - {\mathop{\rm cov}} ered}}{{Total - time - elapsed}} = \frac{{{d_1} + {d_2} + {d_3} + ...}}{{{t_1} + {t_2} + {t_3} + ..}} = \frac{{{v_1}{t_1} + {v_2}{t_2} + {v_3}{t_3} + ...}}{{{t_1} + {t_2} + {t_3} + ...}}\)
Special Cases:
When a particle moves the first half of a speed of \({v_1}\) and second half of the distance at speed \({v_2}\) then, \({v_{av}} = \frac{{2{v_1}{v_2}}}{{{v_1} + {v_2}}}\)
When a particle covers one third distance at speed \({v_1}\), next one third at speed \({v_2}\) and last one third at speed \({v_3}\), then, \({v_{av}} = \frac{{3{v_1}{v_2}{v_3}}}{{{v_1}{v_2} + {v_2}{v_3} + {v_1}{v_3}}}\)
Instantaneous Speed:
It is the speed of a particle at particular instant. When we say "speed", it usually means instantaneous speed.
The instantaneous speed is average speed for infinitesimally small time interval (\(\Delta t \to 0\)). Thus, instantaneous speed \(v = \mathop {\lim }\limits_{\Delta t \to \infty } \frac{{\Delta S}}{{\Delta t}} = \frac{{dS}}{{dt}}\)
Velocity:
Rate of change of position in a particular direction i.e., rate of displacement with time is called velocity.
(1) It is a vector quantity.
(2) Dimension: \(\left[ {{M^0}{L^1}{T^{ - 1}}} \right]\)
(3) In S.I system, Its unit is m/sec and in C.G.S system its unit is cm/sec
(4) Types:
Uniform Velocity:
A particle is said to have uniform velocity, if magnitude as well as direction of its velocity remains same and this is possible only when the particle moves in same straight line without changing its direction.
Non-uniform Velocity:
A particle is said to have non-uniform velocity, if either of magnitude or direction or both are changed.
Average Velocity:
It is defined as the ratio of displacement to time taken by the body. \(\overrightarrow {{v_{av}}} = \frac{{\overrightarrow {\Delta r} }}{{\Delta t}}\)
Instantaneous Velocity:
Instantaneous velocity is defined as rate of change of position vector of particles with time ar a certain instant of time.
Instantaneous velocity = \(\overrightarrow v = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \overrightarrow r }}{{\Delta t}} = \frac{{dr}}{{dt}}\)
If position of a particle at an instant \(t\) is \(\overrightarrow r = x\hat i + y\hat j + z\hat k\), Then,
x component of velocity is \({v_x} = \frac{{dx}}{{dt}}\)
y component of velocity is \({v_y} = \frac{{dy}}{{dt}}\)
z component of velocity is \({v_z} = \frac{{dz}}{{dt}}\)
Thus, The velocity of the particle is, \(v = {v_x}\hat i + {v_y}\hat j + {v_z}\hat k\) = \(\frac{{dx}}{{dt}}\hat i + \frac{{dy}}{{dt}}\hat j + \frac{{dz}}{{dt}}\hat k\)
Some Important Point:
(1) Average velocity may or may not be equal to instantaneous velocity.
(2) If body moves with constant velocity, the instantaneous velocity is equal to average velocity.
(3) The instantaneous speed is equal to modulus of instantaneous velocity.
(4) Distance travelled by the particle is \(S = \int {\left| {\overrightarrow v } \right|dt} \)
(5) \(x\) component of displacement is \(\Delta x = \int {{v_x}dt} \)
\(y\) component of displacement is \(\Delta y = \int {{v_y}dt} \)
\(z\) component of displacement is \(\Delta z = \int {{v_z}dt} \)
Thus, displacement of particle is \(\overrightarrow {\Delta r} = \Delta x\hat i + \Delta y\hat j + \Delta z\hat k\)
(6) If particle moves on a straight line (along X axis), then, \(\overrightarrow v = \frac{{d\overrightarrow x }}{{dt}}\)
(7) The area of velocity-time graph gives displacement.
(8) The area of speed-time graph gives distance.
(9) The slope of tangent at position-time graph at a particular instant gives instantaneous velocity at that instant.
Comparison between instantaneous speed and instantaneous velocity:
(1) Instantaneous velocity is always tangential to the path followed by the particle. When a stone is thrown from a point O then, at point of projection the instantaneous velocity of stone is \({v_1}\), at point A the instantaneous velocity of stone is \({v_2}\), similarly at point B and C are \({v_3}\) and \({v_4}\) respectively. Direction of these velocities can be found out by drawing a tangent on the trajectory at o given point.
(2) A particle may have constant instantaneous speed but variable instantaneous velocity. When a particle is performing uniform circular motion then for every instant of its circular motion its speed remains constant but velocity change at every instant.
(3) The magnitude of instantaneous velocity is equal to the instantaneous speed.
(4) If a particle is moving with constant velocity then, its average velocity and instantaneous velocity are always equal.
(5) If displacement is given as a function of time, then time derivative of displacement will give velocity.
Comparison between average speed and average velocity:
(1) Average speed is scalar while average velocity is a vector both having same units and dimension.
(2) Average speed or velocity depends on time interval over which it is defined.
(3) For a given time interval average velocity is single valued while average speed can have many values depending on path followed.
(4) If after motion body come back to its initial position then, \(\overrightarrow {{v_{av}}} = \overrightarrow 0 \) (As \(\overrightarrow {\Delta r} = 0\) ) but \({v_{av}} > 0\) and finite as (\(\overrightarrow {\Delta S} > 0\))
(5) For a moving body average speed can never be negative, or zero (unless \(t \to 0\) ) while average velocity can be i.e., \({v_{av}}\) > 0 while \(\overrightarrow {{v_{av}}} = or < 0\)
Acceleration:
The time rate of change of velocity of an object is called acceleration of the object.
(1) It is a vector quantity. Its direction is same as that of change in velocity (not of the velocity.)
(2) There are three possible ways by which change in velocity may occur.
(3) Dimension: \(\left[ {{M^0}{L^1}{T^{ - 2}}} \right]\)
Acceleration:
The time rate of change of velocity of an object is called acceleration of the object.
(1) It is a vector quantity. Its direction is same as that of change in velocity (not of the velocity.)
(2) There are three possible ways by which change in velocity may occur.
| When only direction of velocity changes | When only magnitude of velocity changes | When both magnitude and direction of velocity changes |
|---|---|---|
| Acceleration perpendicular to velocity | Acceleration parallel or anti-parallel to velocity | Acceleration has two components one is perpendicular to velocity and another parallel or anti-parallel to velocity |
| Example: Uniform circular motion | Example: Motion under gravity | Example: Projectile motion |
(4) Its S.I units is m/\({s^2}\) and its C.G.S unit is \(cm/{s^2}\)
(5) Type of Acceleration:
Uniform Acceleration:
A body is said to have uniform acceleration if magnitude and direction of the acceleration remains constant during particle motion.
Average Acceleration:
\({a_{av}} = \frac{{\Delta \overrightarrow v }}{{\Delta t}} = \frac{{\left( {{v_2} - {v_1}} \right)}}{{\Delta t}}\) The direction of average acceleration vector is the direction of the change in velocity vector as \(\overrightarrow a = \frac{{\Delta \overrightarrow v }}{{\Delta t}}\)
Instantaneous Acceleration:
\(\overrightarrow a = \mathop {\lim }\limits_{\Delta t \to 0} \frac{{\Delta \overrightarrow v }}{{\Delta t}} = \frac{{d\overrightarrow v }}{{dt}}\)
For a moving body there is no relation between the direction of instantaneous velocity and direction of acceleration.
Example:
(i) In a uniform circular motion \(\theta = 90^\circ \) always
(ii) In a projectile motion \(\theta \) is variable for every point of trajectory.
(6) If a force \(\overrightarrow F \) acts on a particle of mass \(m\), by Newton's second law, acceleration \(\overrightarrow a = \frac{{\overrightarrow F }}{m}\)
(7) By definition \(\overrightarrow a = \frac{{d\overrightarrow v }}{{dt}} = \frac{d}{{dt}}\left( {\frac{{dx}}{{dt}}} \right) = \frac{{{d^2}x}}{{d{t^2}}}\)
That is, if \(x\) is given as a function of time, second time derivative of displacement gives acceleration.
(8) If velocity is given as a function of position, then by chain rule
\(a = \frac{{dv}}{{dt}} = \frac{{dv}}{{dx}} \times \frac{{dx}}{{dt}} = v\frac{{dv}}{{dx}}\)
(9) If a particle is accelerated for a time \({t_1}\) by acceleration \({a_1}\) and for time \({t_2}\) by acceleration \({a_2}\), then average acceleration is \({a_{av}} = \frac{{{a_1}{t_1} + {a_2}{t_2}}}{{{t_1} + {t_2}}}\)
(10) Acceleration can be positive, zero or negative. Positive acceleration means velocity increasing with time, zero acceleration means velocity is uniform constant while negative acceleration (retardation) means velocity is decreasing with time.
(11) For motion of a body under gravity, acceleration will be equal to "g", where "g" is the acceleration due to gravity. Its normal value is \(9.8m/{s^2}\) or \(980cm/{s^2}\) or \(32feet/{s^2}\)
A body is free to move in space. In this case, the initial position of body is taken as origin. Any convenient co-ordinate system is chosen. Let us suppose that at an instant \(t\), the body is at point P (x, y, z). The position vector of the body is \(\overrightarrow r = x\hat i + y\hat j + z\hat k\).
Thus velocity, \(\overrightarrow v = \frac{{d\overrightarrow r }}{{dt}} = \frac{{dx}}{{dt}}\hat i + \frac{{dy}}{{dt}}\hat j + \frac{{dz}}{{dt}}\hat k\)
In this way the velocity along X axis is, \({v_x} = \frac{{dx}}{{dt}}\) and acceleration along X axis is \({a_x} = \frac{{d{v_x}}}{{dt}}\)
And velocity along Y axis is \({v_y} = \frac{{dy}}{{dt}}\) and acceleration along Y axis is \({a_y} = \frac{{d{v_y}}}{{dt}}\)
And velocity along \(z\) axis is \({v_z} = \frac{{dz}}{{dt}}\) and the acceleration is \({a_z} = \frac{{d{v_z}}}{{dt}}\)
Thus the acceleration of the body is \(\overrightarrow a = {a_x}\hat i + {a_y}\hat j + {a_z}\hat k\)
Discussion:
(1.1) If \({a_x} = \) constant then,
\({v_x} = {u_x} + {a_x}t\)
\(x = {u_x} + \frac{1}{2}{a_x}{t^2}\)
\({v_x}^2 = {u_x}^2 + 2{a_x}x\)
(1.2) If \({a_x}\) is variable then,
\(x = \int {{v_x}dt} \)
\(\int {d{v_x} = \int {{a_x}dt} } \)
(2.1) If \({a_y} = \) is constant then,
\({v_y} = {u_y} + {a_y}t\)
\(y = {u_y}t + \frac{1}{2}{a_y}{t^2}\)
\({v_y}^2 = {u_y}^2 + 2{a_y}y\)
(2.2) If \({a_y}\) is variable then,
\(y = \int {{v_y}dt} \)
\(\int {d{v_y} = \int {{v_y}dt} } \)
(3.1) If \({a_z}\) is constant then,
\({v_z} = {u_z} + {a_z}t\)
\(z = {u_z}t + \frac{1}{2}{a_z}{t^2}\)
\({v_z}^2 = {u_z}^2 + 2{a_z}z\)
(3.2) If \({a_z}\) is variable then,
\(z = \int {{v_z}dt} \)
\(\int {d{v_z} = \int {{v_z}dt} } \)
If the motion of the body takes place in XY plane, then, \({a_z} = 0,{v_z} = 0,{u_z} = 0\)
Problem Solving Strategy:
Motion in a Straight Line (Uniform Velocity):
(1) \(S = vt\)
(2) \(a = 0\)
Motion in a Straight Line (Uniform Acceleration):
(1) \(S = \left( {\frac{{u + v}}{2}} \right)t\)
(2) \(s = ut + \frac{1}{2}a{t^2}\)
(3) \({v^2} = {u^2} + 2as\)
(4) \(v = u + at\)
(5) \({S_n} = u + \frac{1}{2}a\left( {2n - 1} \right)\)
Motion in a straight Line (Variable Acceleration):
(1) If \(a = f\left( t \right)\) then, \(a = \frac{{dv}}{{dt}}\)
(2) If \(a = f\left( s \right)\) then, \(a = v\frac{{dv}}{{ds}}\)
(3) If \(a = f\left( v \right)\) then, \(a = \frac{{dv}}{{dt}}\)
(4) \(v = \frac{{ds}}{{dt}}\)
(5) \(s = \int {vdt} \)
(6) \(v = \int {adt} \)
Motion in a Straight Line (Uniform Velocity):
(1) \(S = vt\)
(2) \(a = 0\)
Motion in a Straight Line (Uniform Acceleration):
(1) \(S = \left( {\frac{{u + v}}{2}} \right)t\)
(2) \(s = ut + \frac{1}{2}a{t^2}\)
(3) \({v^2} = {u^2} + 2as\)
(4) \(v = u + at\)
(5) \({S_n} = u + \frac{1}{2}a\left( {2n - 1} \right)\)
Motion in a straight Line (Variable Acceleration):
(1) If \(a = f\left( t \right)\) then, \(a = \frac{{dv}}{{dt}}\)
(2) If \(a = f\left( s \right)\) then, \(a = v\frac{{dv}}{{ds}}\)
(3) If \(a = f\left( v \right)\) then, \(a = \frac{{dv}}{{dt}}\)
(4) \(v = \frac{{ds}}{{dt}}\)
(5) \(s = \int {vdt} \)
(6) \(v = \int {adt} \)
COMMENTS