ROTATIONAL MECHANICS (ঘূর্ণন গতিবিজ্ঞান)

LEARN FAST ABOUT: ROTATIONAL MECHANICS দৃঢ় বস্তুর ঘূর্ণন গতিবিজ্ঞান: CONCEPT OF \(\omega \) AND \(\alpha \):  \(\omega \) is def...

LEARN FAST ABOUT: ROTATIONAL MECHANICS

দৃঢ় বস্তুর ঘূর্ণন গতিবিজ্ঞান:

CONCEPT OF \(\omega \) AND \(\alpha \):

 \(\omega \) is defined as the angular velocity of the body. The angular velocity of a body expresses the degree of rotation of the body. The higher the angular velocity, the faster does the body rotates. Angular velocity is closely associated with revolution per second. If a body rotates faster, it should cover a greater number of revolutions per second. The quantity \(\omega \) and revolutions per second are associated with the formula,

Revolution per second \( = \frac{\omega }{{2\pi }}\)

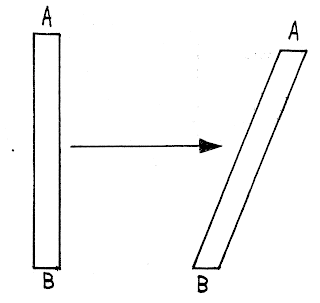
Here point A and B moves same distance.
Assume a scale AB shown above. Consider two points on the scale A and B, initially at rest. After a period of time A and B have moved some distance. 
In this case A and B have moved same distance, that the scale has moved straight and has not rotated at all.
Such kind of motion are called pure translatory motion. Here only physical parameter involved is translational velocity. Here we observe that all point have the same velocity.


Now consider an another situation:

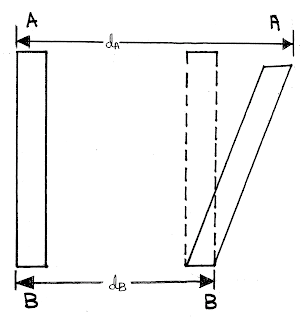
Here point A has moved more than B. Now the motion is no longer only translatory. The scale has rotate now. We associates the concept of angular velocity. Some interesting points to note are:
(1) Angular velocity results in change in the angular inclination of the body.

(2) Different points move different distances when a body has angular velocity or angular acceleration.

Here let us assume that point A and B move by distance \({d_A}\) and \({d_B}\).
We can now describe the motion of the body by using two parameter.
Translatory Motion: The distance moved by all points in the scale is equal to \({d_B}\).
Rotation of the scale: For small value of \(\theta \), we can say that \(\theta  = \frac{{{d_A} - {d_B}}}{l}\), where \(l\) is the length of the scale.
Therefore pure translation of the scale is \({d_B}\) and pure rotation of the scale is \(\frac{{{d_A} - {d_B}}}{l}\).
Now we assume that the points A and B travel the distance in time \(t\).
So, in pure translational component of the velocity is \(\frac{{{d_B}}}{t}\) and amount of rotation per unit time is \( = \frac{\theta }{t} = \frac{{{d_A} - {d_B}}}{{lt}}\).
The amount of rotation per unit time is called angular velocity.
So, \(\omega  = \frac{\theta }{t} = \frac{{{d_A} - {d_B}}}{{lt}} = \frac{{\frac{{{d_A}}}{t} - \frac{{{d_B}}}{t}}}{l} = \frac{{{v_A} - {v_B}}}{l}\)
In other words, angular velocity is equal to difference in the velocity of two point divided by the distance between them.
If both the point have same velocity, the difference will be zero and the angular velocity is also zero.
Let us consider two points, (1) the center of mass and (2) any other point in the scale.
The equation would be \(\omega  = \frac{{{v_x} - {v_{cm}}}}{l}\)
or, \({v_x} - {v_{cm}} = \omega l\)
or, \({v_x} = {v_{cm}} + \omega l\)
This is the popular equation that combines rotation and translation motion into a single value. Here you need to perform vector addition between theses two value.
\({v_x} = {v_{cm}} + \omega l\)